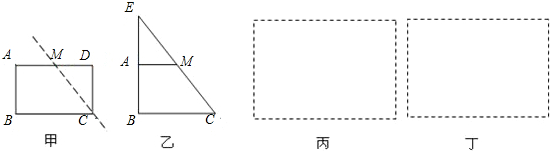
题目内容
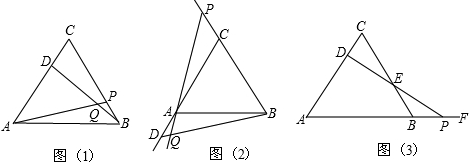
（1）如图（1）所示，以
的边
、
为边分别向外作正方形
和正方形
，连结
，试判断与
面积之间的关系，并说明
理由．
（2）园林小路，曲径通幽，如图（２）所示，小路由白色的正方形大理石和黑色的三角形大理石铺成．已知中间的所有正方形的面积之和是
平方米，内圈的所有三角形的面积之和是
平方米，这条小路一
共占地多少平方米？
解：（1）与的面积相等.
理由如下：过点
作
于
，过点
作
交
的延长线于
，则
.
四边形和四边形都是正方形，
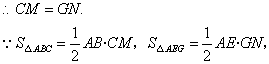
（2）由（1）知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和，
这条小路的占地面积为
平方米．
练习册系列答案
阅读快车系列答案
相关题目
