题目内容
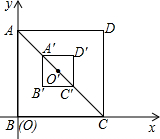
如图,正方形OEFG和正方形ABCD的是位似图形,若点A的坐标为(2,2),位似中心的坐标是(-4,0),则点F的坐标为______.
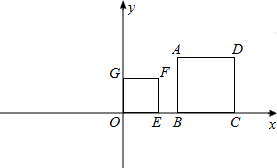

连接DF并延长到x轴一点P,即为位似中心,
∵正方形ABCD,点A的坐标为(2,2),
∴AB=BC=CD=AD=2,
∴OC=4,
∵EF∥DC,
∴△PFE∽△PDC,
∴
=
,
∴
=
,
又∵EO=EF,
解得:EF=
,
∴F点的坐标是(
,
).
故答案为:(
,
).

∵正方形ABCD,点A的坐标为(2,2),
∴AB=BC=CD=AD=2,
∴OC=4,
∵EF∥DC,
∴△PFE∽△PDC,
∴
| PE |
| PC |
| EF |
| DC |
∴
| 4+EO |
| 4+4 |
| EF |
| 2 |
又∵EO=EF,
解得:EF=
| 4 |
| 3 |
∴F点的坐标是(
| 4 |
| 3 |
| 4 |
| 3 |
故答案为:(
| 4 |
| 3 |
| 4 |
| 3 |


练习册系列答案
相关题目