Question

【题目】如图 1，AB∥CD，点 E 在 AB 上，点 M 在 CD 上，点 F 在直线 AB，CD 之间，连接 EF、FM， EF⊥FM，∠CMF=140°.

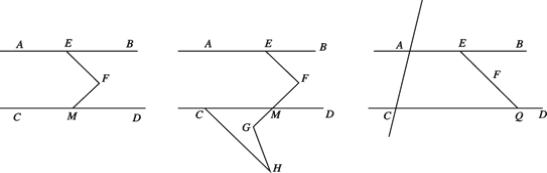
图 1 图 2 图 3

（1）直接写出∠AEF 的度数为 ________；

（2）如图 2，延长 FM 到 G，点 H 在 FG 的下方，连接 GH，CH，若∠FGH=∠H+90°， 求∠MCH 的度数；

（3）如图 3，作直线 AC，延长 EF 交 CD 于点 Q，P 为直线 AC 上一动点，探究∠PEQ，∠PQC 和∠EPQ 的数量关系，请直接给出结论.（题中所有角都是大于 0°小于 180°的角）

Answer 1

【答案】（1）130°；（2）50°；（3）当P点在CD的下方时，∠PEQ+∠EPQ+∠PQC=130°．当P点在CD的上方时，∠PEQ+∠EPQ+∠PQC=230°．

【解析】

（1）延长FP交AB于点Q，根据三角形的外角性质和平行线性质证明即可；

（2）延长HG交CD于点Q，根据三角形的外角性质和平行线性质证明即可；

（3）过P点作PN∥AB，根据平行线性质证明即可．

（1）延长MF交AB于点N，如图1，

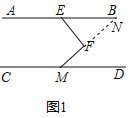
∵AB∥CD，

∴∠CMF+∠ENF=180°，

∴∠ANF=180°-140°=40°，

∵EF⊥FM，

∴∠EFN=90°，

∴∠AEF=∠ANF+∠EFN=40°+90°=130°；

故答案为：130°．

（2）延长HG交CD于点Q，如图2，

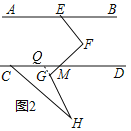
∵∠CMF=140°．

∴∠FMD=180°-140°=40°，

∴∠CMG=40°，

∵∠MQH=∠H+∠HCM，∠FGH=∠H+90°，

∴∠FGH=∠MQH+∠CMG=∠H+∠HCM+∠CMG，

∴∠HCM+∠CMG=90°，

∴∠MCH=90°-40°=50°；

（3）过P点作PN∥AB，如图3，

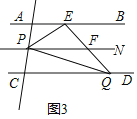
由（1）可知，∠AEF=130°，

∴∠AEP+∠PEQ=130°，

∵AB∥CD，

∴AB∥PN∥CD，

∴∠AEP=∠EPN，∠NPQ=∠PQC，

∴∠EPN=∠EPQ-∠NPQ=∠EPQ-∠PQC，

∴∠PEQ+∠EPQ-∠PQC=130°．

当P点在CD的下方时，∠PEQ+∠EPQ+∠PQC=130°．

当P点在CD的上方时，∠PEQ+∠EPQ+∠PQC=230°．