题目内容
 22、如图,△ABD、△BCD都是等边三角形,E、F分别是AD、CD上的两个动点,且满足DE=CF.
22、如图,△ABD、△BCD都是等边三角形,E、F分别是AD、CD上的两个动点,且满足DE=CF.(1)求证:△BDE≌△BCF;(2)指出△BCF是由△BDE经过如何变换得到的?
分析:(1)结合已知条件,根据全等三角形判定定理SAS,即可求证△BDE≌△BCF;
(2)根据旋转的性质,知道∠DBC即可.
(2)根据旋转的性质,知道∠DBC即可.
解答:证明:∵△ABD、△BCD都是等边三角形,
∴∠BDA=∠C=60°,BD=BC(3分)
又∵DE=CF(5分)
∴△BDE≌△BCF;(6分)
(2)∵△BCD都是等边三角形
∴∠DBC=60°
∴△BCF是由△BDE绕点B顺时针旋转60°得到的.(9分)
∴∠BDA=∠C=60°,BD=BC(3分)
又∵DE=CF(5分)
∴△BDE≌△BCF;(6分)
(2)∵△BCD都是等边三角形
∴∠DBC=60°
∴△BCF是由△BDE绕点B顺时针旋转60°得到的.(9分)
点评:本题主要考查了全等三角形的判定定理,等边三角形的性质,旋转的性质

练习册系列答案
相关题目
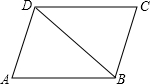 如图,△ABD≌△CDB,下面结论中不正确的是( )
如图,△ABD≌△CDB,下面结论中不正确的是( )| A、△ABD和△CDB的面积相等 | B、∠A+∠ABD=∠C+∠CBD | C、△ABD和△CDB的周长相等 | D、AD∥BC,且AD=BC |
 4、如图,∠ABD=90°,直线
4、如图,∠ABD=90°,直线 15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是
15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是 如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求
如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求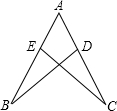 如图,△ABD≌△ACE,那么点B与点
如图,△ABD≌△ACE,那么点B与点