题目内容
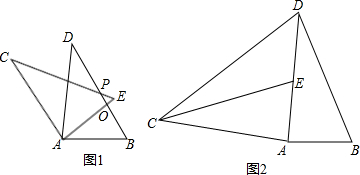
如图①所示,已知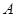 、
、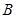 为直线
为直线 上两点,点
上两点,点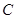 为直线
为直线 上方一动点,连接
上方一动点,连接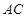 、
、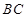 ,分别以
,分别以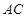 、
、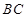 为边向
为边向 外作正方形
外作正方形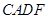 和正方形
和正方形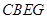 ,过点
,过点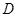 作
作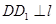 于点
于点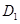 ,过点
,过点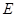 作
作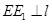 于点
于点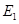 .
.
【小题1】如图②,当点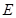 恰好在直线
恰好在直线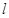 上时(此时
上时(此时 与
与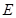 重合),试说明
重合),试说明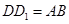 ;
;
【小题2】在图①中,当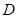 、
、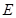 两点都在直线
两点都在直线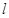 的上方时,试探求三条线段
的上方时,试探求三条线段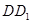 、
、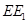 、
、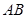 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
【小题3】如图③,当点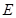 在直线
在直线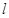 的下方时,请直接写出三条线段
的下方时,请直接写出三条线段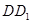 、
、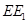 、
、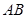 之间的数量关系.(不需要证明)
之间的数量关系.(不需要证明)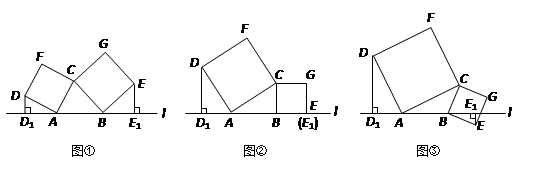
【小题1】在正方形 中,∵
中,∵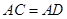 ,
,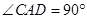 ,
,
∴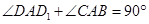
又∵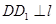 , ∴
, ∴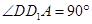 ,∴
,∴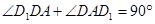 ,
,
∴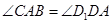
又∵四边形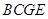 为正方形,∴
为正方形,∴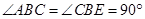 ,∴
,∴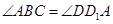
在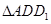 与
与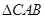 中,
中, ,
,
∴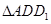 ≌
≌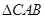 ,∴
,∴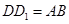
【小题1】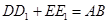
过点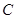 作
作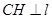 ,垂足为
,垂足为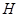 ,
,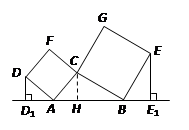
由(1)知: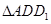 ≌
≌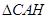 ,
,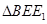 ≌
≌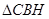 、
、
∴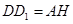 ,
,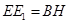 ,∴
,∴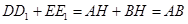 、
、
【小题1】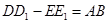
解析【小题1】由四边形CADF、CBEG是正方形,可得AD=CA,∠DAC=∠ABC=90°,又由同角的余角相等,求得∠ADD1=∠CAB,然后利用AAS证得△ADD1≌△CAB,根据全等三角形的对应边相等,即可得DD1=AB;
【小题1】首先过点C作CH⊥AB于H,由DD1⊥AB,可得∠DD1A=∠CHA=90°,由四边形CADF是正方形,可得AD=CA,又由同角的余角相等,求得∠ADD1=∠CAH,然后利用AAS证得
△ADD1≌△CAH,根据全等三角形的对应边相等,即可得DD1=AH,同理EE1=BH,则可得AB=DD1+EE1.
【小题1】证明方法同(2),易得AB=DD1-EE1

练习册系列答案
相关题目
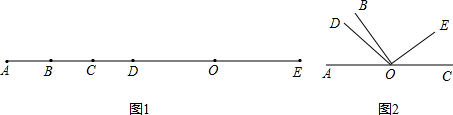

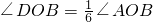 ,
,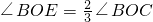 ,∠DOB与∠BOE互余,求∠AOB和∠BOC.
,∠DOB与∠BOE互余,求∠AOB和∠BOC.