Question

如图所示，在半径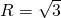的圆中∠C=30°，则AB的值为

1. A.
   
2. B.
   
3. C.
   
4. D.
   

Answer 1

B
分析：连接OD，OE，由同弧所对的圆心角等于所对圆周角的2倍，根据圆周角∠C=30°，求出圆心角∠DOE为60°，又OD=OE，可得出三角形ODE为等边三角形，根据半径的长得到DE的长，由OA垂直于DE，根据垂径定理得到B为DE的中点，由DE的长求出DB的长，在直角三角形OBD中，由OD及DB的长，利用勾股定理求出OB的长，再由OA-OB即可求出AB的长．
解答：连接OD，OE，如图所示：
∵圆心角∠DOE与圆周角∠C都对，且∠C=30°，
∴∠DOE=2∠C=60°，
又∵OD=OE=，
∴△ODE为等边三角形，
∴DE=OD=OE=，
∵OA⊥DE，
∴B为DE的中点，
∴DB=EB=DE=，
在Rt△OBD中，OD=，BD=，
根据勾股定理得：OB==，
又OA=，
则AB=OA-OB=-．
故选B．
点评：此题考查了垂径定理，勾股定理，圆周角定理，以及等边三角形的判定与性质，熟练掌握定理及性质是解本题的关键．