题目内容
设a是正整数,如果二次函数y=2x2+(2a+23)x+10-7a和反比例函数y=| 11-3a | x |
分析:根据二次函数y=2x2+(2a+23)x+10-7a和反比例函数y=
的图象有公共整点,可以判断出△=(a+18)2-224是一个完全平方数.将原式分解后可得(a+18+k)(a+18-k)=224,从而判断出a+18+k与a+18-k的奇偶性相同,将224分解成两个奇偶性相同的数的积,与a+18+k和a+18-k对应相等,列出方程组即可.
| 11-3a |
| x |
解答:解:联立方程组
,
消去y得2x2+(2a+23)x+10-7a=
,即2x3+(2a+23)x2+(10-7a)x+3a-11=0,
分解因式得(2x-1)[x2+(a+12)x+11-3a]=0(1)
如果两个函数的图象有公共整点,则方程(1)必有整数根,
从而关于x的一元二次方程x2+(a+12)x+11-3a=0(2)必有整数根,
所以一元二次方程(2)的判别式△应该是一个完全平方数,
而△=(a+12)2-4(11-3a)=a2+36a+100=(a+18)2-224.
所以(a+18)2-224应该是一个完全平方数,
设(a+18)2-224=k2(其中k为非负整数),则(a+18)2-k2=224,即(a+18+k)(a+18-k)=224.
显然a+18+k与a+18-k的奇偶性相同,且a+18+k≥18,而224=112×2=56×4=28×8,
所以
或
或
解得
或
或
.
而a是正整数,所以只可能
或
当a=39时,方程(2)即x2+51x-106=0,它的两根分别为2和-53,易求得两个函数的图象有公共整点(2,-53)和(-53,2).
当a=12时,方程(2)即x2+24x-25=0,它的两根分别为1和-25,易求得两个函数的图象有公共整点(1,-25)和(-25,1).
|
消去y得2x2+(2a+23)x+10-7a=
| 11-3a |
| x |
分解因式得(2x-1)[x2+(a+12)x+11-3a]=0(1)
如果两个函数的图象有公共整点,则方程(1)必有整数根,
从而关于x的一元二次方程x2+(a+12)x+11-3a=0(2)必有整数根,
所以一元二次方程(2)的判别式△应该是一个完全平方数,
而△=(a+12)2-4(11-3a)=a2+36a+100=(a+18)2-224.
所以(a+18)2-224应该是一个完全平方数,
设(a+18)2-224=k2(其中k为非负整数),则(a+18)2-k2=224,即(a+18+k)(a+18-k)=224.
显然a+18+k与a+18-k的奇偶性相同,且a+18+k≥18,而224=112×2=56×4=28×8,
所以
|
|
|
|
|
|
而a是正整数,所以只可能
|
|
当a=39时,方程(2)即x2+51x-106=0,它的两根分别为2和-53,易求得两个函数的图象有公共整点(2,-53)和(-53,2).
当a=12时,方程(2)即x2+24x-25=0,它的两根分别为1和-25,易求得两个函数的图象有公共整点(1,-25)和(-25,1).
点评:此题考查了和整数相关的函数.此题需要进行逻辑推理,给出的思维空间很小,需要很高的数学水平才能顺利解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

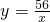 ,如果两个函数的图象的交点都是整点(横坐标和纵坐标都是整数的点),求a的值.
,如果两个函数的图象的交点都是整点(横坐标和纵坐标都是整数的点),求a的值.