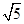题目内容
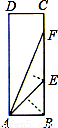
 小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是
小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是
- A.
 +1
+1 - B.
 +1
+1 - C.2.5
- D.

B
分析:根据翻折变换的性质得出AB=BE,∠AEB=∠EAB=45°,∠FAB=67.5°,进而得出tan∠FAB=tan67.5°= 得出答案即可.
得出答案即可.
解答: ∵将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,
∵将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,
∴AB=BE,∠AEB=∠EAB=45°,
∵还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,
∴AE=EF,∠EAF=∠EFA=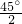 =22.5°,
=22.5°,
∴∠FAB=67.5°,
设AB=x,
则AE=EF= x,
x,
∴tan∠FAB=tan67.5°= =
= =
= +1.
+1.
故选:B.
点评:此题主要考查了翻折变换的性质,根据已知得出∠FAB=67.5°以及AE=EF是解题关键.
分析:根据翻折变换的性质得出AB=BE,∠AEB=∠EAB=45°,∠FAB=67.5°,进而得出tan∠FAB=tan67.5°=
 得出答案即可.
得出答案即可.解答:
 ∵将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,
∵将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,∴AB=BE,∠AEB=∠EAB=45°,
∵还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,
∴AE=EF,∠EAF=∠EFA=
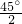 =22.5°,
=22.5°,∴∠FAB=67.5°,
设AB=x,
则AE=EF=
 x,
x,∴tan∠FAB=tan67.5°=
 =
= =
= +1.
+1.故选:B.
点评:此题主要考查了翻折变换的性质,根据已知得出∠FAB=67.5°以及AE=EF是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过 点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出
小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过 点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出 (2012•连云港)小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( )
(2012•连云港)小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( )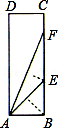
 +1
+1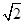 +1
+1 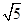
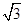 +1 B.
+1 B.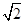 +1 C.2.5 D.
+1 C.2.5 D.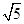
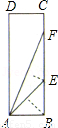
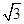 +1 B.
+1 B.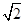 +1 C.2.5
D.
+1 C.2.5
D.