Question

【题目】如图，△ABC中，AB=AC=26，BC=20，AD是BC边上的中线，AD=24，F是AD上的动点，E是AC边上的动点，则CF+EF的最小值为 ．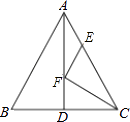

Answer 1

【答案】
【解析】解：作BE⊥AC垂足为E，交AD于F，此时CF+EF最小．

理由如下：∵AB=AC，AD是中线，

∴AD⊥BC，

∴FB=FC，

∴CF+EF=BF+EF，

∵线段BE是垂线段，根据垂线段最短，

∴点E、点F、就是所找的点．

∵ BCAD= ACBE，

∴ ×20×24= ×26×BE，

∴BE= ，

∴CF+EF的最小值=BE= ，

故答案为 ．

根据等腰三角形的三线合一，得到AD⊥BC，FB=FC，CF+EF=BF+EF，由线段BE是垂线段，根据垂线段最短，得到点E、点F、就是所找的点，求出CF+EF的最小值=BE的值.