题目内容
等腰三角形ABC的面积为10,AB=AC=5,那么BC= 或 .
考点:等腰三角形的性质
专题:压轴题
分析:作出图形,过点A作AD⊥BC于D,设BC=2x,根据等腰三角形三线合一的性质可得BD=CD=
BC,然后根据勾股定理列式求出AD,再根据三角形的面积公式列式计算求出x的值,即可得解.
| 1 |
| 2 |
解答: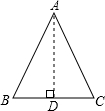 解:如图,过点A作AD⊥BC于D,
解:如图,过点A作AD⊥BC于D,
设BC=2x,则BD=CD=
BC=x,
在Rt△ABD中,AD=
=
,
S△ABC=
BC•AD=
×2x
=10,
整理得,x4-25x2+100=0,
解得x2=20或x2=5,
所以,x=2
或
,
BC=4
或2
.
故答案为:4
;2
.
 解:如图,过点A作AD⊥BC于D,
解:如图,过点A作AD⊥BC于D,设BC=2x,则BD=CD=
| 1 |
| 2 |
在Rt△ABD中,AD=
| AB2-BD2 |
| 25-x2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 25-x2 |
整理得,x4-25x2+100=0,
解得x2=20或x2=5,
所以,x=2
| 5 |
| 5 |
BC=4
| 5 |
| 5 |
故答案为:4
| 5 |
| 5 |
点评:本题考查了等腰三角形三线合一的性质,勾股定理三角形的面积,解一元二次方程,综合题,但难度不大,作出图形更形象直观.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
两圆内切,圆心距为8,若一圆的直径为6,则另一圆的直径为( )
| A、2 | B、5 | C、10 | D、14 |
 如图,AB是⊙0的直径,AC是弦.∠BAC=40°.过圆心O作OD⊥AC交AC于点D.连接DC.则∠DCA=
如图,AB是⊙0的直径,AC是弦.∠BAC=40°.过圆心O作OD⊥AC交AC于点D.连接DC.则∠DCA=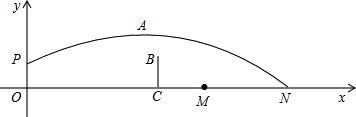
 如图,将正方形CDFE绕点C逆时针旋转90°后与正方形ABCD重合,那么点F的对应点是点
如图,将正方形CDFE绕点C逆时针旋转90°后与正方形ABCD重合,那么点F的对应点是点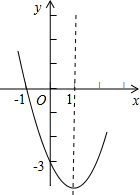 已知,抛物线y=ax2+bx+c的部分图象如图,则下列说法:①当x=1时,函数值最大;②当-1<x<3时,y<0;③a+b+c=-4;④方程ax2+bx+c+5=0无实数根.其中正确的有( )
已知,抛物线y=ax2+bx+c的部分图象如图,则下列说法:①当x=1时,函数值最大;②当-1<x<3时,y<0;③a+b+c=-4;④方程ax2+bx+c+5=0无实数根.其中正确的有( )