题目内容
图（1）、图（2）、图（3）分别表示甲、乙、丙三人由A地到B地的路线图．已知：
甲的路线为：A?C?B．
乙的路线为：A?D?E?F?B，其中E为AB的中点．
丙的路线为：A?I?J?K?B，其中J在AB上，且AJ＞JB．
若符号?表示「直线前进」，则根据图（1）、图（2）、图（3）的数据，判断三人行进路线长度的大小关系为何
- A.甲=乙=丙
- B.甲＜乙＜丙
- C.乙＜丙＜甲
- D.丙＜乙＜甲
A
分析：由角的度数可以知道（2）（3）中的两个三角形的对应边都是平行的，所以图二，图三中的三角形都和图一中的三角形相似．而且图二三角形全等，图三三角形相似．
解答：
解：根据以上分析：所以图二可得AE=BE，AD=EF，DE=BF，
∵AE=BE=
AB，∴AD=EF=AC，DE=BF=BC．∴甲=乙
图三与图一中，三个三角形相似，所以
，
=
=
，
∵AJ+BJ=AB，∴
==
，
∵AI+JK=AC，IJ+BK=BC，
又∵甲行进路线的总长度为：AC+CB，
丙行进路线的总长度为：AI+IJ+JK+KB=（AI+JK）+（IJ+BK）=AC+CB，
∴甲=丙．
∴甲=乙=丙．
故选A．
点评：本题主要利用三角形的相似和全等，可求得线段的关系．
分析：由角的度数可以知道（2）（3）中的两个三角形的对应边都是平行的，所以图二，图三中的三角形都和图一中的三角形相似．而且图二三角形全等，图三三角形相似．
解答：
解：根据以上分析：所以图二可得AE=BE，AD=EF，DE=BF，∵AE=BE=
AB，∴AD=EF=AC，DE=BF=BC．∴甲=乙图三与图一中，三个三角形相似，所以
，==，∵AJ+BJ=AB，∴
==，∵AI+JK=AC，IJ+BK=BC，
又∵甲行进路线的总长度为：AC+CB，
丙行进路线的总长度为：AI+IJ+JK+KB=（AI+JK）+（IJ+BK）=AC+CB，
∴甲=丙．
∴甲=乙=丙．
故选A．
点评：本题主要利用三角形的相似和全等，可求得线段的关系．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
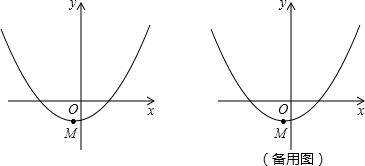
（x+1）2-2图象的顶点为M，点P是x轴上一个动点，将二次函数y1的图象绕点P旋转180°得到一个新的二次函数y2的图象，且旋转前后的两个函数图象相伴随，y2的图象的顶点为N．
类似地，图2所示的算筹图我们可以表述为（ ）
B．
C．
D．
