题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]()
![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴与
,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)设直线![]() 与直线
与直线![]() 关于该抛物线的对称轴对称,
关于该抛物线的对称轴对称,
①求直线![]() 的解析式
的解析式
②若该抛物线在![]() 这一段位于直线
这一段位于直线![]() 的上方,并且在
的上方,并且在![]() 这一段位于直线
这一段位于直线![]() 的下方,求该抛物线的解析式.
的下方,求该抛物线的解析式.
【答案】(1)点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)令![]() 求出
求出![]() 的值,即可得到点A的坐标,求出对称轴解析式,即可得到点B的坐标;
的值,即可得到点A的坐标,求出对称轴解析式,即可得到点B的坐标;
(2)求出点A关于对称轴的对称点(2,-2),然后设直线l的解析式为![]() (k≠0),利用待定系数法求一次函数解析式解答即可;
(k≠0),利用待定系数法求一次函数解析式解答即可;
(3)根据二次函数的对称性判断在2<x<3这一段与在-1<x<0这一段关于对称轴对称,然后判断出抛物线与直线l的交点的横坐标为-1,代入直线l求出交点坐标,然后代入抛物线求出m的值即可得到抛物线解析式.
(1) ∵当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为(0,-2),
的坐标为(0,-2),
∴抛物线的对称轴为直线![]() ;
;
∴点B的坐标为(1,0);
(2)①由题意,点A(0,-2)关于直线![]() 的对称点
的对称点![]() 的坐标为(2,-2),
的坐标为(2,-2),
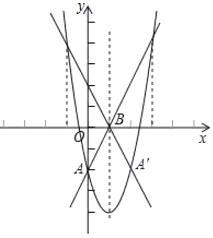
设直线![]() 的解析式为
的解析式为![]() ,
,
∵点![]() (1,0)和
(1,0)和![]() (2,-2)在直线
(2,-2)在直线![]() 上,
上,
∴![]() ,
,
解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ;
;
②∵抛物线的对称轴为直线![]() ,
,
∴抛物线在2<x<3这一段与在-1<x<0这一段关于对称轴对称,
结合图象可以观察到抛物线在-2<x<-1这一段位于直线![]() 的上方,在-1<x<0这一段位于直线
的上方,在-1<x<0这一段位于直线![]() 的下方,
的下方,
∴抛物线与直线![]() 的交点的横坐标为-1,
的交点的横坐标为-1,
当![]() 时,
时,![]() ,
,
所以,抛物线过点(-1,4),
当![]() 时,
时,![]() ,
,
解得![]() ,
,
∴抛物线的解析式为![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】小夏同学从家到学校有![]() ,
,![]() 两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计,早高峰期间,乘坐![]() 线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填
线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填![]() 或
或![]() )线路.
)线路.