题目内容
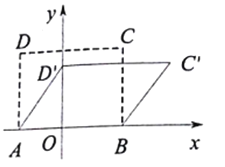
【题目】定义:在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 平行于
平行于![]() 轴.若
轴.若![]() 的三个顶点都在二次函数
的三个顶点都在二次函数![]() 的图像上,则称
的图像上,则称![]() 为该二次函数图像的“伴随三角形”.
为该二次函数图像的“伴随三角形”.![]() 为抛物
为抛物![]() 的“伴随三角形”.
的“伴随三角形”.
(1)若点![]() 是抛物线与
是抛物线与![]() 轴的交点,求点
轴的交点,求点![]() 的坐标.
的坐标.
(2)若点![]() 在该抛物线的对称轴上,且到边
在该抛物线的对称轴上,且到边![]() 的距离为2,求
的距离为2,求![]() 的面积.
的面积.
(3)设![]() 两点的坐标分别为
两点的坐标分别为![]() ,比较
,比较![]() 与
与![]() 的大小,并求
的大小,并求![]() 的取值范围.
的取值范围.
(4)![]() 是抛物线
是抛物线![]() 的“伴随三角形”,点
的“伴随三角形”,点![]() 在点
在点![]() 的左侧,且
的左侧,且![]() ,点
,点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的2倍,设该抛物线在
的横坐标的2倍,设该抛物线在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围和
的取值范围和![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)4;(3)当
;(2)4;(3)当![]() 时,
时,![]() ,当
,当![]() ,
,![]() 且
且![]() 时,
时,![]() ;(4)
;(4)![]() ,
,![]()
【解析】
(1)由![]() 轴及伴随三角形的定义,抛物线的对称轴可得答案.
轴及伴随三角形的定义,抛物线的对称轴可得答案.
(2)由题意得:![]() 为抛物线的顶点,求解
为抛物线的顶点,求解![]() 的坐标,结合已知条件,得到
的坐标,结合已知条件,得到![]() 的坐标,进而求出
的坐标,进而求出![]() 与
与![]() 上的高可得
上的高可得![]() 的面积.
的面积.
(3)先写出![]() 两点坐标,由
两点坐标,由![]() 轴,当
轴,当![]() 为抛物线的顶点时,
为抛物线的顶点时,![]() 不存在,当
不存在,当![]() 两点的纵坐标相等时,
两点的纵坐标相等时,![]() 不存在,求解对应的
不存在,求解对应的![]() 的值,再利用二次函数的性质分段得到答案,
的值,再利用二次函数的性质分段得到答案,
(4)由![]() 求解抛物线的对称轴
求解抛物线的对称轴![]() ,分
,分![]() 讨论最高点的位置,求解最高点在纵坐标,代入
讨论最高点的位置,求解最高点在纵坐标,代入![]() ,利用二次函数的性质求解
,利用二次函数的性质求解![]() 的范围,再求解
的范围,再求解![]() 面积的最大值.
面积的最大值.
(1)当![]() 时,
时,![]() ,∴
,∴![]()
对称轴: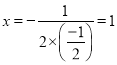 ,
,
![]() 轴,
轴,
∴![]()
(2)![]() 在抛物线上,也在对称轴上,
在抛物线上,也在对称轴上,
![]() 为抛物线的顶点,
为抛物线的顶点,
当![]() 时,
时,![]()
∴![]()
![]() 到边
到边![]() 的距离为2,
的距离为2,
∴![]()
∴当![]() 时,
时,![]()
![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∴![]()
(3)![]() ,
,![]()
①当![]() 时,
时,![]() 为抛物线的顶点,所以
为抛物线的顶点,所以![]() 不成立,
不成立,
②当![]()
解得:![]() ,
,![]() ,
,
此时结合题意:![]() 轴,
轴,![]() 不成立
不成立
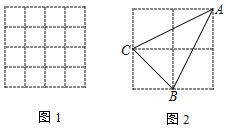
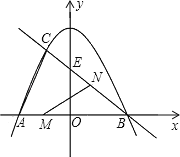
③当![]() 时,如图
时,如图
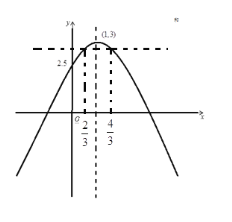
结合图像得:![]() ,
,
④当![]() 且
且![]() 时,结合图像可得:
时,结合图像可得:![]()
⑤当![]() 时,结合图像可得:
时,结合图像可得:![]()
综上:
当![]() 时,
时,![]()
当![]() ,
,![]() 且
且![]() 时,
时,![]() .
.
(4)![]()
![]()
![]()
![]()
顶点![]()
①当![]() 时,即
时,即![]()
当![]() 时
时
![]()
![]()
![]()
![]()
当![]()
![]()
解得:![]()
由二次函数的性质得:![]()
由![]() ,
,
![]()
![]()
![]()
![]()
![]() 为任意数
为任意数
∴![]()
②当![]() 时,
时,
即:![]() ,顶点的纵坐标最大,
,顶点的纵坐标最大,
![]()
![]() ,
,
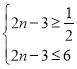
∴![]()
综上![]()
当![]() 时,
时,![]()
![]() 轴,
轴,
![]()
![]() 此时
此时![]() ,
,
![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 时
时
![]()
![]()
∴![]()
此时面积最大,最大面积是![]()

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
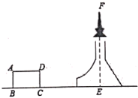
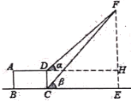
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)