题目内容

已知抛物线 y=（m-1）x²+（m-2）x-1与x轴交于A、B两点．
（1）求m的取值范围；
（2）若m＞1，且点A在点B的左侧，OA：OB=1：3，试确定抛物线的解析式；
（3）设（2）中抛物线与y轴的交点为C，过点C作直线l∥x轴，将抛物线在y轴左侧的部分沿直线l翻折，抛物线的其余部分保持不变，得到一个新图象．请你结合新图象回答：当直线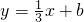 $数学公式$ 与新图象只有一个公共点P（x₀，y₀）且 y₀≤7时，求b的取值范围．

解：（1）∵抛物线y=（m-1）x²+（m-2）x-1与x轴交于A、B两点，
∴ $\text{[math]}$
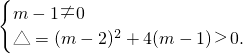
由①得m≠1，
由②得m≠0，
∴m的取值范围是m≠0且m≠1．
（2）∵点A、B是抛物线y=（m-1）x²+（m-2）x-1与x轴的交点，
∴令y=0，即（m-1）x²+（m-2）x-1=0．
解得 x₁=-1， $\text{[math]}$ ．
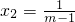∵m＞1，
∴ $\text{[math]}$ ．
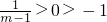∵点A在点B左侧，
∴点A的坐标为（-1，0），点B的坐标为 $\text{[math]}$ ．
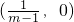∴OA=1，OB= $\text{[math]}$ ．
∵OA：OB=1：3，
∴ $\text{[math]}$ ．
∴ $\text{[math]}$ ．
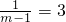∴抛物线的解析式为 $\text{[math]}$ ．
（3）∵点C是抛物线 $\text{[math]}$ 与y轴的交点，
∴点C的坐标为（0，-1）．
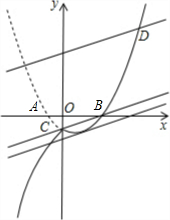
依题意翻折后的图象如图所示．
令y=7，即 $\text{[math]}$ ．
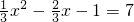解得x₁=6，x₂=-4．
∴新图象经过点D（6，7）．
当直线 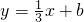$\text{[math]}$ 经过D点时，可得b=5．
当直线 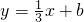$\text{[math]}$ 经过C点时，可得b=-1．
当直线 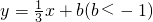$\text{[math]}$ 与函数 $\text{[math]}$
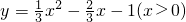
的图象仅有一个公共点P（x₀，y₀）时，得 $\text{[math]}$ ．
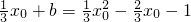整理得 $\text{[math]}$ ．
由△=（-3）²-4（-3b-3）=12b+21=0，得 $\text{[math]}$ ．
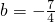结合图象可知，符合题意的b的取值范围为-1＜b≤5或 $\text{[math]}$ ．
分析：（1）抛物线 y=（m-1）x²+（m-2）x-1与x轴交于A、B两点，即在解析式中令y=0，得到一个一元二次方程，这个方程有两个不同的解，根据一元二次方程的根的判别式即可求解；
（2）首先求抛物线与x轴的交点坐标，根据OA：OB=1：3，即可得到关于m的方程，从而求解；
（3）首先求得抛物线与x轴的交点坐标，以及函数当y=7时，函数的横坐标，则根据图象可以得到：直线在过C的直线与过D的直线之间，或在与抛物线只有一个交点的直线的下边，以及根的判别式即可求得m的范围．
点评：本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点．主要考查学生数形结合的数学思想方法．