题目内容
 如图,⊙O的直径AB=4,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设四边形ABCD的面积为S,则S的取值范围为________.
如图,⊙O的直径AB=4,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设四边形ABCD的面积为S,则S的取值范围为________.
S≥8
分析:根据切线的性质得到它们都和直径垂直,得到AM与NB平行,作直角梯形的另一高,构造一个直角三角形,根据切线长定理和勾股定理列方程,再表示出关于y的函数关系式;根据直角梯形的面积公式表示梯形的面积,再根据基本不等式即可求出S的范围.
解答: 解:∵AB是直径,AM、BN是切线,
解:∵AB是直径,AM、BN是切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
过点D作DF⊥BC于F,则AB∥DF,
∴四边形ABFD为矩形.
∴DF=AB=4,BF=AD=x,
∵DE、DA,CE、CB都是切线,
∴根据切线长定理,得DE=DA=x,CE=CB=y,
在Rt△DFC中,DF=4,DC=DE+CE=x+y,CF=BC-BF=y-x,
∴(x+y)2=42+(y-x)2,
化简,得y= (x>0).
(x>0).
则四边形的面积S= AB(AD+BC)=
AB(AD+BC)= ×4×(x+
×4×(x+ ),即S=2(x+
),即S=2(x+ )=2x+
)=2x+ (x>0).
(x>0).
∵2x+ ≥2
≥2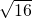 =8,当且仅当x=2时,等号成立.
=8,当且仅当x=2时,等号成立.
∴x+ ≥8,即S≥8.
≥8,即S≥8.
故答案为:S≥8
点评:此题考查了切线的性质,勾股定理,梯形的面积公式,矩形的判定与性质,基本不等式的运用,以及切线长定理,熟练掌握切线的性质是解本题的关键.
分析:根据切线的性质得到它们都和直径垂直,得到AM与NB平行,作直角梯形的另一高,构造一个直角三角形,根据切线长定理和勾股定理列方程,再表示出关于y的函数关系式;根据直角梯形的面积公式表示梯形的面积,再根据基本不等式即可求出S的范围.
解答:
 解:∵AB是直径,AM、BN是切线,
解:∵AB是直径,AM、BN是切线,∴AM⊥AB,BN⊥AB,
∴AM∥BN,
过点D作DF⊥BC于F,则AB∥DF,
∴四边形ABFD为矩形.
∴DF=AB=4,BF=AD=x,
∵DE、DA,CE、CB都是切线,
∴根据切线长定理,得DE=DA=x,CE=CB=y,
在Rt△DFC中,DF=4,DC=DE+CE=x+y,CF=BC-BF=y-x,
∴(x+y)2=42+(y-x)2,
化简,得y=
 (x>0).
(x>0).则四边形的面积S=
 AB(AD+BC)=
AB(AD+BC)= ×4×(x+
×4×(x+ ),即S=2(x+
),即S=2(x+ )=2x+
)=2x+ (x>0).
(x>0).∵2x+
 ≥2
≥2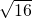 =8,当且仅当x=2时,等号成立.
=8,当且仅当x=2时,等号成立.∴x+
 ≥8,即S≥8.
≥8,即S≥8.故答案为:S≥8
点评:此题考查了切线的性质,勾股定理,梯形的面积公式,矩形的判定与性质,基本不等式的运用,以及切线长定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
 已知:如图,⊙O的直径AB与弦CD相交于E,
已知:如图,⊙O的直径AB与弦CD相交于E,
 如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于
如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于 如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:
如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论: (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC= 如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是
如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是