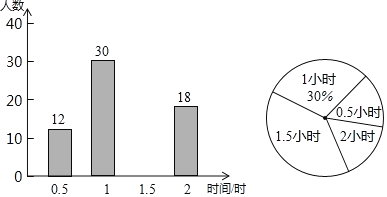
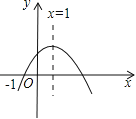ЬтФПФкШн
ЁОЬтФПЁПШчЭМЫљЪОЃЌЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ОЙ§
ОЙ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЎЙ§Еу
ЃЎЙ§Еу![]() зї
зї![]() жсНЛХзЮяЯпгкЕу
жсНЛХзЮяЯпгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊЕу
жсЃЌДЙзуЮЊЕу![]() ЃЎЕу
ЃЎЕу![]() ЪЧЫФБпаЮ
ЪЧЫФБпаЮ![]() ЕФЖдНЧЯпЕФНЛЕуЃЌЕу
ЕФЖдНЧЯпЕФНЛЕуЃЌЕу![]() дк
дк![]() жсИКАыжсЩЯЃЌЧв
жсИКАыжсЩЯЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЌВЂжБНгаДГіЫФБпаЮ![]() ЕФаЮзДЃЛ
ЕФаЮзДЃЛ
ЃЈ2ЃЉЕБЕу![]() ЁЂ
ЁЂ![]() Дг
Дг![]() ЁЂ
ЁЂ![]() СНЕуЭЌЪБГіЗЂЃЌОљвдУПУы
СНЕуЭЌЪБГіЗЂЃЌОљвдУПУы![]() ИіГЄЖШЕЅЮЛЕФЫйЖШби
ИіГЄЖШЕЅЮЛЕФЫйЖШби![]() ЁЂ
ЁЂ![]() ЗНЯђдЫЖЏЃЌЕу
ЗНЯђдЫЖЏЃЌЕу![]() дЫЖЏЕН
дЫЖЏЕН![]() ЪБ
ЪБ![]() ЁЂ
ЁЂ![]() СНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЕФЪБМфЮЊ
СНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЕФЪБМфЮЊ![]() УыЃЌдкдЫЖЏЙ§ГЬжаЃЌвд
УыЃЌдкдЫЖЏЙ§ГЬжаЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЫФЕуЮЊЖЅЕуЕФЫФБпаЮЕФУцЛ§ЮЊ
ЫФЕуЮЊЖЅЕуЕФЫФБпаЮЕФУцЛ§ЮЊ![]() ЃЌЧѓГі
ЃЌЧѓГі![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЬнаЮЃПШєДцдкЃЌжБНгаДГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЬнаЮЃПШєДцдкЃЌжБНгаДГіЕу![]() ЕФзјБъЃЛВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФзјБъЃЛВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЮЊе§ЗНаЮЃЛЃЈ2ЃЉЕБ
ЮЊе§ЗНаЮЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЃЈ3ЃЉдкХзЮяЯпЩЯДцдкЕу
ЃЛЃЈ3ЃЉдкХзЮяЯпЩЯДцдкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЬнаЮЃЎ
ЮЊЖЅЕуЕФЫФБпаЮЪЧЬнаЮЃЎ
ЁОНтЮіЁП
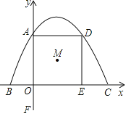
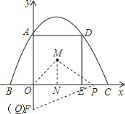
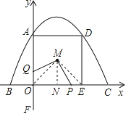
ЃЈ1ЃЉгЩХзЮяЯпy=ax2+bx+cОЙ§AЃЈ0ЃЌ4ЃЉЁЂBЃЈ-2ЃЌ0ЃЉЁЂCЃЈ6ЃЌ0ЃЉШ§ЕуЃЌАбШ§ЕузјБъДњШыХзЮяЯпБэДяЪНжаЃЌСЊСЂЗНГЬНтГіaЁЂbЁЂcЃЛ
ЃЈ2ЃЉЙ§MзїMNЁЭOEгкNЃЌдђMN=2ЃЌгЩЬтвтПЩжЊCP=FQ=tЃЌЕБ0Ёмt<2ЪБЃЌOP=6ЃtЃЌOQ=2ЃtЃЌСаГіSгыtЕФЙиЯЕЪНЃЌЕБt=2ЪБЃЌQгыOжиКЯЃЌЕуMЁЂOЁЂPЁЂQВЛФмЙЙГЩЫФБпаЮЃЌЕБ2<t<6ЪБЃЌСЌНгMOЃЌMEдђMO=MEЧвЁЯQOM=ЁЯPEM=45ЁуЃЌПЩжЄШ§НЧаЮШЋЕШЃЌНјЖјМЦЫуГіШ§НЧаЮУцЛ§ЃЛ
ЃЈ3ЃЉШєBЁЂCЁЂFЁЂNЮЊЖЅЕуЕФЫФБпаЮЪЧЬнаЮЃЌдђЫФБпаЮгаСНБпЦНааЃЌЩшГіNЕуЕФзјБъЃЌЗжРрЬжТлСНБпЦНааЪБNЕузјБъТњзуЕФЬѕМўЃЌНјЖјЧѓГіNЕузјБъЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпОЙ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЫФБпаЮ![]() ЮЊе§ЗНаЮЃЎ
ЮЊе§ЗНаЮЃЎ
ЃЈ2ЃЉСЌНг![]() ЃЎ
ЃЎ
ИљОнЬтвтЃЌПЩжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпдЫЖЏЕФЪБМфЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Й§![]() зї
зї![]() гк
гк![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() жиКЯЃЌЕу
жиКЯЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ВЛФмЙЙГЩЫФБпаЮЃЌ
ВЛФмЙЙГЩЫФБпаЮЃЌ
ЕБ![]() ЪБЃЌСЌНг
ЪБЃЌСЌНг![]() ЃЌ
ЃЌ![]() дђ
дђ![]() Чв
Чв![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЫФБпаЮ![]() ЕФУцЛ§
ЕФУцЛ§![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЗжШ§жжЧщПіЃК
Ђйвд![]() ЮЊЕзБпЪБЃЌОЙ§Еу
ЮЊЕзБпЪБЃЌОЙ§Еу![]() зї
зї![]() ЕФЦНааЯпЃЌгыХзЮяЯпНЛгкЕу
ЕФЦНааЯпЃЌгыХзЮяЯпНЛгкЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛ
ЃЛ
Ђквд![]() ЮЊЕзБпЪБЃЌОЙ§Еу
ЮЊЕзБпЪБЃЌОЙ§Еу![]() зї
зї![]() ЕФЦНааЯпЃЌгыХзЮяЯпНЛгкЕу
ЕФЦНааЯпЃЌгыХзЮяЯпНЛгкЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛ
ЃЛ
Ђлвд![]() ЮЊЕзБпЪБЃЌОЙ§Еу
ЮЊЕзБпЪБЃЌОЙ§Еу![]() зї
зї![]() ЕФЦНааЯпЃЌгыХзЮяЯпНЛгкЕу
ЕФЦНааЯпЃЌгыХзЮяЯпНЛгкЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЙЪдкХзЮяЯпЩЯДцдкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЪЙвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЬнаЮЃЎ
ЮЊЖЅЕуЕФЫФБпаЮЪЧЬнаЮЃЎ