题目内容
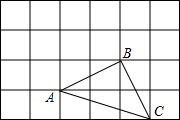
①在图中，四边形ABCD是正方形，使△ABE逆时针旋转变到△ADF的位置，确定它的旋转中心和旋转角的度数；
②指出图中线段BE与DF之间的关系，并说明理由．
②指出图中线段BE与DF之间的关系，并说明理由．
（1）根据正方形的性质可知：△AFD≌△AEB，
即AE=AF=4，∠EAF=90°，∠EBA=∠FDA；
可得旋转中心为点A；旋转角度为90°或270°；
（2）BE与DF是垂直关系；
理由：∵∠EAF=90°，∠EBA=∠FDA，
∴延长BE与DF相交于点G，则∠GDE+∠DEG=90°，
∴BE⊥DF，
即BE与DF是垂直关系．
即AE=AF=4，∠EAF=90°，∠EBA=∠FDA；
可得旋转中心为点A；旋转角度为90°或270°；
（2）BE与DF是垂直关系；
理由：∵∠EAF=90°，∠EBA=∠FDA，
∴延长BE与DF相交于点G，则∠GDE+∠DEG=90°，
∴BE⊥DF，
即BE与DF是垂直关系．
练习册系列答案
相关题目
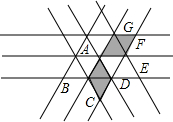
，点C在x轴上方，如图．
