题目内容
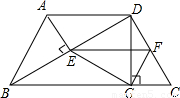
 附加题:如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,求此梯形的中位线长.
附加题:如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,求此梯形的中位线长.
分析:作DE∥AC,交BC的延长线于E,则四边形ACED为平行四边形,根据已知及平行四边形的性质得梯形的中位线等于BE的一半,根据勾股定理可求得BE的长,从而不难求得其中位线的长.
解答: 解:作DE∥AC,交BC的延长线于E,则四边形ACED为平行四边形,
解:作DE∥AC,交BC的延长线于E,则四边形ACED为平行四边形,
∴AD=CE,
∵AC⊥BD,
∴∠BDE=90°,
∴梯形的中位线长=
(AD+BC)=
(CE+BC)=
BE,
∵BE=
=
=15.
∴梯形的中位线长=
×15=7.5.
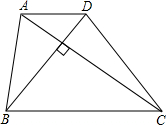
 解:作DE∥AC,交BC的延长线于E,则四边形ACED为平行四边形,
解:作DE∥AC,交BC的延长线于E,则四边形ACED为平行四边形,∴AD=CE,
∵AC⊥BD,
∴∠BDE=90°,
∴梯形的中位线长=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BE=
| BD2+DE2 |
| 92+122 |
∴梯形的中位线长=
| 1 |
| 2 |
点评:解答此题的关键是作出辅助线,构造出平行四边形和直角三角形,将求梯形中位线转化为求直角三角形斜边的问题来解答.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
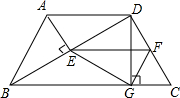
 附加题:如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A出发沿AD边向点D以1cm/s的速度移动,点Q从点C出发沿CB向点B以2cm/s的速度移动,若点P、Q分别从点A、C同时出发,设移动时间为t s,则t为何值时,梯形PQCD是等腰梯形?
附加题:如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A出发沿AD边向点D以1cm/s的速度移动,点Q从点C出发沿CB向点B以2cm/s的速度移动,若点P、Q分别从点A、C同时出发,设移动时间为t s,则t为何值时,梯形PQCD是等腰梯形? 附加题:如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A出发沿AD边向点D以1cm/s的速度移动,点Q从点C出发沿CB向点B以2cm/s的速度移动,若点P、Q分别从点A、C同时出发,设移动时间为t s,则t为何值时,梯形PQCD是等腰梯形?
附加题:如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A出发沿AD边向点D以1cm/s的速度移动,点Q从点C出发沿CB向点B以2cm/s的速度移动,若点P、Q分别从点A、C同时出发,设移动时间为t s,则t为何值时,梯形PQCD是等腰梯形?