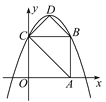��Ŀ����
����Ŀ��������C1��y1=mx2��4mx+2n��1��ƽ����x���ֱ�߽���A��B���㣬��A������Ϊ����1��2��������ͼ��������½��ۣ��ٶԳ���Ϊֱ��x=2������������y�ύ������Ϊ��0����1������m��![]() ������������C2��y2=ax2��a��0�����߶�ABǡ��һ�������㣬��a��ȡֵ��Χ��
������������C2��y2=ax2��a��0�����߶�ABǡ��һ�������㣬��a��ȡֵ��Χ��![]() ��a��2���ݲ���ʽmx2��4mx+2n��0�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ������������ȷ���۵ĸ����У� ��
��a��2���ݲ���ʽmx2��4mx+2n��0�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ������������ȷ���۵ĸ����У� ��

A. 2�� B. 3�� C. 4�� D. 5��
���𰸡�B
��������
���������ߵĶԳ���ֱ�߹�ʽ��������öԳ���ֱ�ߣ�������������������Ľ���������ص㣬�ó�C�������Ϊ����0��2n-1��;��A�����꣨-1.2�����������߽���ʽ��������:2n=3-5m,�ٴ���![]() �������ã�
�������ã�![]()
����֪��������x�����������㣬��������б�ʽӦ�ô���0���Ӷ��г�����m�IJ���ʽ�����m��ȡֵ��Χ���������ߵĶԳ��ԣ�B�������ΪB��5��2������![]() ��ͼ��ֱ����A��Bʱ�������߶ηֱ�����ֻ��һ�������㣬��ʱ��a��ֵ�ֱ�Ϊ
��ͼ��ֱ����A��Bʱ�������߶ηֱ�����ֻ��һ�������㣬��ʱ��a��ֵ�ֱ�Ϊ![]() ,�Ӷ��ó�a��ȡֵ��Χ������ʽ
,�Ӷ��ó�a��ȡֵ��Χ������ʽ![]() �Ľ���Կ����ǣ�������
�Ľ���Կ����ǣ�������![]() λ��ֱ��y=-1�Ϸ��IJ��֣����ʱx��ȡֵ��Χ������
λ��ֱ��y=-1�Ϸ��IJ��֣����ʱx��ȡֵ��Χ������![]() ����ֵ��Χ֮�ڣ�Ȼ�������жϼ���.
����ֵ��Χ֮�ڣ�Ȼ�������жϼ���.
�������ߵĶԳ���Ϊֱ��![]() ��������ȷ��
��������ȷ��
�ڵ�x=0ʱ��y=2n-1,�ʢڴ���
�� ��A�����꣨-1.2�����������߽���ʽ��������:2n=3-5m
�ٴ���![]() �������ã�
�������ã�![]()
����֪��������x�����������㣬��
![]() ��������:
��������:![]()
��ã�m>![]() ����������.
����������.
���������ߵĶԳ��ԣ�B�������ΪB��5��2��
�����߶ηֱ�����ֻ��һ��������
��ʱ��a��ֵ�ֱ�Ϊ![]()
�ó�a��ȡֵ��Χ,��![]() ���ʢ���ȷ.
���ʢ���ȷ.
�ݲ���ʽ![]() �Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ����,�ʢ���ȷ,��ѡB.
�Ľ���Ϊ����C1���Ա�����ȡֵʱ����Ӧ�ĺ���ֵ��Ϊ����,�ʢ���ȷ,��ѡB.

����Ŀ��Ϊ�˲μ�����������Сѧ����ʫ�ʴ������ijУ���꼶������ѧ��������Ԥѡ�����а���ǰ5��ѧ���ijɼ����ٷ��ƣ��ֱ�Ϊ���ˣ�1����86��85��77��92��85���ˣ�2����79��85��92��85��89��ͨ�����ݷ������б����£�
�༶ | ƽ���� | ��λ�� | ���� | ���� |
�ˣ�1�� | 85 | b | c | 22.8 |
�ˣ�2�� | a | 85 | 85 | 19.2 |
��1��ֱ��д������a��b��c��ֵ��
��2�������������ݷ���������Ϊ�ĸ���ǰ5��ͬѧ�ijɼ��Ϻã�˵�����ɣ�