题目内容
3.为了落实党中央提出的“惠民政策”,我市今年计划开发建设A,B两种户型的“廉租房”共40套,投入资金不低于270万元,又不超过296万元,开发建设办公室预算:一套A型“廉租房”的造价为10万元,一套B型“廉租房”的造价为4.8万元.(1)请问有几种开发建设方案?
(2)在投入资金最少的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低1万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
分析 (1)设建设A型x套,B型(40-x)套,然后根据投入资金不超过296万元,又不低于270万元列出不等式组,求出不等式组的解集,再根据x是正整数解答;
(2)设总投资W元,建设A型x套,B型(40-x)套,然后根据总投资等于A、B两个型号的投资之和列式函数关系式,再根据一次函数的增减性解答;
设再次建设A、B两种户型分别为a套、b套,根据再建设的两种户型的资金等于(2)中方案节省的资金列出二元一次方程,再根据a、b都是正整数求解即可.
解答 解:(1)设建设A型x套,则B型(40-x)套,根据题意得,
$\left\{\begin{array}{l}{10x+4.8(40-x)≥270}\\{10x+4.8(40-x)≤296}\end{array}\right.$
解得:15≤x≤20,
∵x为正整数,
∴x=15、16、17、18、19、20.
答:共有6种方案;
(2)设总投资W万元,建设A型x套,则B型(40-x)套,
W=10x+4.8×(40-x)=5.2x+192,
∵5.2>0,
∴W随x的增大而增大,
∴当x=15时,W最小,此时W最小=5.2×15+192=270万元;
设再次建设A、B两种户型分别为a套、b套,
则(10-1)a+(4.8-0.3)b=15×1+(40-15)×0.3,
整理得,2a+b=5,
∵a,b为正整数,
∴a=1时,b=3,
a=2时,b=1,
所以,再建设方案:①A型住房1套,B型住房3套;②A型住房2套,B型住房1套.
点评 本题考查了一次函数的应用,一元一次不等式组的应用,读懂题目信息,理清题中不等量关系,列出不等式组是解题的关键,(2)利用一次函数的增减性求最值要注意自变量的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,直线l1∥l2,∠1=55°,则∠2的度数是( )
如图,直线l1∥l2,∠1=55°,则∠2的度数是( )
 如图,直线l1∥l2,∠1=55°,则∠2的度数是( )
如图,直线l1∥l2,∠1=55°,则∠2的度数是( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
15.已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
12.一组数据2、3、4、4、5、5、5的中位数和众数分别是( )
| A. | 3.5,5 | B. | 4,4 | C. | 4,5 | D. | 4.5,4 |
13.在△ABC中,AB=12$\sqrt{2}$,AC=13,cos∠B=$\frac{{\sqrt{2}}}{2}$,则BC边长为( )
| A. | 7 | B. | 8 | C. | 8或17 | D. | 7或17 |
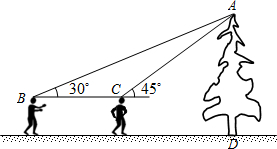 某校初三学生去社会实践,在风景区看到一棵汉白杨树,好高哟,数学老师说请小明和小华同学用数学知识测量,全体同学计算这棵树多高,下面是这两位同学的对话.
某校初三学生去社会实践,在风景区看到一棵汉白杨树,好高哟,数学老师说请小明和小华同学用数学知识测量,全体同学计算这棵树多高,下面是这两位同学的对话.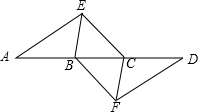 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.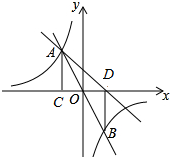 如图,在直角坐标系xOy中,直线y=mx与双曲线y=$\frac{n}{x}$相交于A(-1,a)、B两点,AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,且满足tan∠AOC=2.
如图,在直角坐标系xOy中,直线y=mx与双曲线y=$\frac{n}{x}$相交于A(-1,a)、B两点,AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,且满足tan∠AOC=2.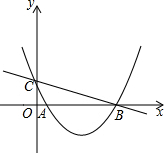 如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.
如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.