Question

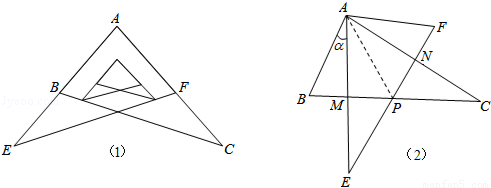
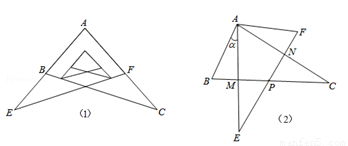
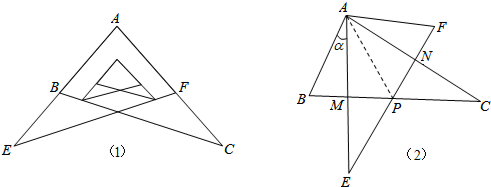
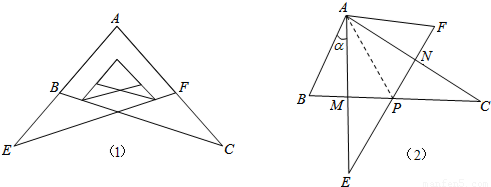
某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．

（1）求证：AM=AN；

（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．

Answer 1

考点：

旋转的性质；全等三角形的判定与性质；菱形的判定．

分析：

（1）根据旋转的性质得出AB=AF，∠BAM=∠FAN，进而得出△ABM≌△AFN得出答案即可；

（2）利用旋转的性质得出∠FAB=120°，∠FPC=∠B=60°，即可得出四边形ABPF是平行四边形，再利用菱形的判定得出答案．

解答：

（1）证明：∵用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），

∴AB=AF，∠BAM=∠FAN，

在△ABM和△AFN中，

，

∴△ABM≌△AFN（ASA），

∴AM=AN；

（2）解：当旋转角α=30°时，四边形ABPF是菱形．

理由：连接AP，

∵∠α=30°，

∴∠FAN=30°，

∴∠FAB=120°，

∵∠B=60°，

∴AF∥BP，

∴∠F=∠FPC=60°，

∴∠FPC=∠B=60°，

∴AB∥FP，

∴四边形ABPF是平行四边形，

∵AB=AF，

∴平行四边形ABPF是菱形．

点评：

此题主要考查了平行四边形的判定以及菱形的判定和全等三角形的判定等知识，根据旋转前后图形大小不发生变化得出是解题关键．