题目内容
已知:如图,E、F分别是平行四边形ABCD的ADBC边上的点,且AE=CF.

(1)求证:△ABE≌△CDF
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
答案:
解析:
解析:
|
证明:(1)∵四边形ABCD是平行四边形, ∴AB=CD,∠A=∠C 又∵AE=CF (2)四边形MFNE是平行四边形 ∵ ∴∠AEB=∠CFD,BE=DF 又∵M、N分别是BE、DF的中点 ∴ME=FN ∵四边形ABCD是平行四边形 ∴∠AEB=∠FBE ∴∠CFD=∠FBE ∴BE∥DF,即ME∥FN ∴四边形MFNE是平行四边形.
|

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

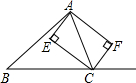 已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F. 21、已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点.
21、已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点.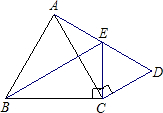 已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形. 已知:如图,E,F分别是?ABCD的边AD,BC的中点.求证:AF=CE.
已知:如图,E,F分别是?ABCD的边AD,BC的中点.求证:AF=CE. 已知,如图,BE、CF分别是△ABC的边AC、AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.请你判断线段AD与AG有什么关系?并证明.
已知,如图,BE、CF分别是△ABC的边AC、AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.请你判断线段AD与AG有什么关系?并证明.