Question

 阅读下面材料：

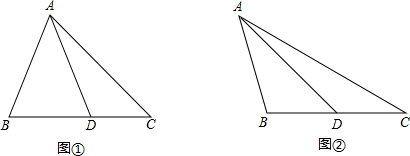
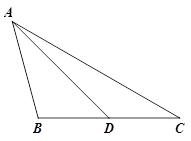
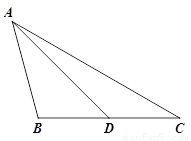
问题：如图①，在△ABC中， D是BC边上的一点，若∠BAD=∠C=2∠DAC=45°，DC=2．求BD的长．

小明同学的解题思路是：利用轴对称，把△ADC进行翻折，再经过推理、计算使问题得到解决．

（1）请你回答：图中BD的长为    ；

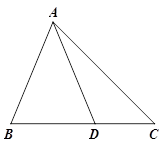
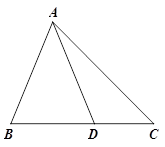
（2）参考小明的思路，探究并解答问题：如图②，在△ABC中，D是BC边上的一点，若∠BAD=∠C=2∠DAC=30°，DC=2，求BD和AB的长．

                                                                                   

图①                                    图②

Answer 1

 解：（1）. ……………………………………………………………………1分

（2）把△ADC沿AC翻折，得△AEC，连接DE，

∴△ADC≌△AEC.

∴∠DAC=∠EAC，∠DCA=∠ECA， DC＝EC.

∵∠BAD=∠BCA=2∠DAC=30°，

∴∠BAD=∠DAE=30°，∠DCE=60°.

∴△CDE为等边三角形. ……………………2分

∴DC＝DE.

在AE上截取AF＝AB，连接DF，

∴△ABD≌△AFD.

∴BD＝DF.

在△ABD中，∠ADB=∠DAC＋∠DCA=45°，

∴∠ADE=∠AED =75°，∠ABD =105°.

∴∠AFD =105°.

∴∠DFE=75°.

∴∠DFE=∠DEF.

∴DF＝DE.  

∴BD＝DC＝2. …………………………………………………………………3分

作BG⊥AD于点G，

∴在Rt△BDG中， .  ……………………………………………4分

∴在Rt△ABG中，.  ……………………………………………5分