题目内容
圆O外一点P与圆心O的距离为4,从P点向圆作切线,若切线长与半径长之差为2,则P点到圆O的最短距离是( )
A、(
| ||
B、(
| ||
C、(3-
| ||
D、(5-
|
分析:首先根据题意作图,由PA是⊙O的切线,根据切线的性质可得OA⊥PA,即可得∠OAP=90°,又由切线长与半径长之差为2,设OA=x,则PA=x+2,根据勾股定理,即可求得方程:x2+(x+2)2=42,解此方程即可求得半径的长,继而求得P点到圆O的最短距离.
解答: 解:连接OA,
解:连接OA,
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵切线长与半径长之差为2,
设OA=x,则PA=x+2,
∵OA2+PA2=OP2,
即x2+(x+2)2=42,
解得:x=
-1.
∴OA=OB=
-1,
∴PB=OP-OB=4-(
-1)=5-
.
故选D.
 解:连接OA,
解:连接OA,∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵切线长与半径长之差为2,
设OA=x,则PA=x+2,
∵OA2+PA2=OP2,
即x2+(x+2)2=42,
解得:x=
| 7 |
∴OA=OB=
| 7 |
∴PB=OP-OB=4-(
| 7 |
| 7 |
故选D.
点评:此题考查了圆的切线的性质与勾股定理的应用.此题难度不大,解题的关键是注意数形结合思想与方程思想的应用,注意辅助线的作法.

练习册系列答案
相关题目
 上关于点A、B的滑动角。
上关于点A、B的滑动角。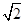 ,求∠APB的度数
,求∠APB的度数
 为
为 外一点,以
外一点,以 于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。
于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。 上关于点A、B的滑动角。
上关于点A、B的滑动角。 ,求∠APB的度数
,求∠APB的度数
 为
为 外一点,以
外一点,以 于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。
于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。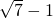 )
) )
) )
) )
)