题目内容
已知二次函数图象的对称轴是x+3=0,图象经过(1,-6),且与y轴的交点为(0,-| 5 | 2 |
(1)求这个二次函数的解析式;
(2)当x为何值时,这个函数的函数值为0;
(3)当x在什么范围内变化时,这个函数的函数值y随x的增大而增大?
分析:①本题实际上已知了三个条件,可设抛物线的一般形式y=ax2+bx+c求解;
②根据函数值为0解答;
③利用对称轴解答这个问题.
②根据函数值为0解答;
③利用对称轴解答这个问题.
解答:解:(1)设抛物线的解析式为y=ax2+bx+c,
由题意可得
,
解得a=-
,b=-3,c=-
,
所以y=-
x2-3x-
.
答:这个二次函数的解析式y=-
x2-3x-
.
(2)令y=0,得-
x2-3x-
=0,
解得:x=-1或-5.
答:当x为-1或-5时,这个函数的函数值为0.
(3)由于对称轴是x=-3,开口向下,
所以当x<-3时,函数的函数值y随x的增大而增大.
答:当x<-3时,函数的函数值y随x的增大而增大.
由题意可得
|
解得a=-
| 1 |
| 2 |
| 5 |
| 2 |
所以y=-
| 1 |
| 2 |
| 5 |
| 2 |
答:这个二次函数的解析式y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)令y=0,得-
| 1 |
| 2 |
| 5 |
| 2 |
解得:x=-1或-5.
答:当x为-1或-5时,这个函数的函数值为0.
(3)由于对称轴是x=-3,开口向下,
所以当x<-3时,函数的函数值y随x的增大而增大.
答:当x<-3时,函数的函数值y随x的增大而增大.
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了二次函数的性质等相关知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知二次函数图象的顶点是(-1,2),且过点
已知二次函数图象的顶点是(-1,2),且过点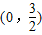 .
.
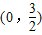 .
.
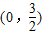 .
.
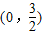 .
.