题目内容
 如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是
如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是
- A.108°
- B.100°
- C.90°
- D.80°
C
分析:根据三角形内角和定理,三角形外角和内角的关系以及等腰三角形的性质,逐步推出∠GEF的度数.
解答:∵∠A=18°,AB=BC=CD=DE=EF,∴∠ACB=18°,
根据三角形外角和外角性质得出∠BCD=108°,
∴∠CBD=∠CDB= ×(180°-108°)=36°,
×(180°-108°)=36°,
∵∠ECD=180°-∠BCD-∠ACB=180°-108°-18°=54°,
∴∠ECD=∠CED=54°
∴∠CDE=180°-54°×2=72°,
∵∠EDF=∠EFD=180°-(∠CDB+∠CDE)=72°,
∴∠DEF=180°-(∠EDF+∠EFD)=36°,
∴∠GEF=180°-(∠CED+∠DEF)=90°,
即∠GEF=90°.
故选C.
点评:此类题考生应该注意的是三角形内角和定理的运用.
分析:根据三角形内角和定理,三角形外角和内角的关系以及等腰三角形的性质,逐步推出∠GEF的度数.
解答:∵∠A=18°,AB=BC=CD=DE=EF,∴∠ACB=18°,
根据三角形外角和外角性质得出∠BCD=108°,
∴∠CBD=∠CDB=
 ×(180°-108°)=36°,
×(180°-108°)=36°,∵∠ECD=180°-∠BCD-∠ACB=180°-108°-18°=54°,
∴∠ECD=∠CED=54°
∴∠CDE=180°-54°×2=72°,
∵∠EDF=∠EFD=180°-(∠CDB+∠CDE)=72°,
∴∠DEF=180°-(∠EDF+∠EFD)=36°,
∴∠GEF=180°-(∠CED+∠DEF)=90°,
即∠GEF=90°.
故选C.
点评:此类题考生应该注意的是三角形内角和定理的运用.

练习册系列答案
相关题目
 10、如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=13:3:2,则∠DPE的度数为( )
10、如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=13:3:2,则∠DPE的度数为( ) 3、如图所示,三角尺和直尺所夹的∠1和∠2的数量关系是( )
3、如图所示,三角尺和直尺所夹的∠1和∠2的数量关系是( ) 19、如图,已知△ABC和△A″B″C″及点O.
19、如图,已知△ABC和△A″B″C″及点O.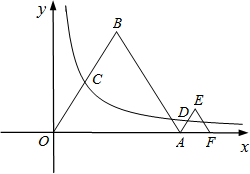 (2012•丽水)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
(2012•丽水)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=