题目内容
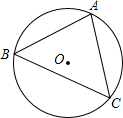 如图,△ABC内接圆于⊙O,∠B=45°,AC=
如图,△ABC内接圆于⊙O,∠B=45°,AC=| 2 |
1
1
.分析:连接OA和OB,根据圆周角定理可知△AOC是等腰直角三角形,在直角三角形AOC中,求出OA的长即可.
解答: 解:连接OA和OB,
解:连接OA和OB,
∵∠B=45°,
∴∠AOC=90°,
∴△AOC是等腰直角三角形,
∵AO2+OC2=AC2,且AC=
,
∴OA=1,
即⊙O半径的长为1.
故答案为1.
 解:连接OA和OB,
解:连接OA和OB,∵∠B=45°,
∴∠AOC=90°,
∴△AOC是等腰直角三角形,
∵AO2+OC2=AC2,且AC=
| 2 |
∴OA=1,
即⊙O半径的长为1.
故答案为1.
点评:本题主要考查了圆周角定理和等腰直角三角形的知识点,解答本题的关键是作辅助线,此题难度不大.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目


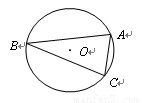
 ,⊙O半径的长为 .
,⊙O半径的长为 .