题目内容
边长为1的正方形 的顶点
的顶点 在
在 轴的正半轴上,如图将正方形
轴的正半轴上,如图将正方形 绕顶点
绕顶点 顺时针旋转
顺时针旋转 得正方形
得正方形 ,使点
,使点 恰好落在函数
恰好落在函数 的图像上,则
的图像上,则 的值为 。
的值为 。

 的顶点
的顶点 在
在 轴的正半轴上,如图将正方形
轴的正半轴上,如图将正方形 绕顶点
绕顶点 顺时针旋转
顺时针旋转 得正方形
得正方形 ,使点
,使点 恰好落在函数
恰好落在函数 的图像上,则
的图像上,则 的值为 。
的值为 。
过点B向x轴引垂线,连接OB,可得OB的长度,进而得到点B的坐标,代入二次函数解析式即可求解.
解:如图,作BE⊥x轴于点E,连接OB,
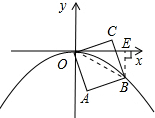
∵正方形OABC绕顶点O顺时针旋转75°,
∴∠AOE=75°,
∵∠AOB=45°,
∴∠BOE=30°,
∵OA=1,
∴OB=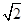 ,
,
∵∠OCB=90°,
∴BE=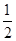 OB=
OB=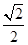 ,
,
∴OE=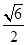 ,
,
∴点B坐标为(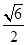 ,-
,-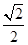 ),
),
代入y=ax2(a<0)得a=-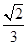 ,
,
解:如图,作BE⊥x轴于点E,连接OB,

∵正方形OABC绕顶点O顺时针旋转75°,
∴∠AOE=75°,
∵∠AOB=45°,
∴∠BOE=30°,
∵OA=1,
∴OB=
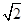 ,
,∵∠OCB=90°,
∴BE=
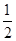 OB=
OB=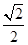 ,
,∴OE=
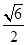 ,
,∴点B坐标为(
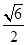 ,-
,-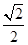 ),
),代入y=ax2(a<0)得a=-
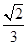 ,
,
练习册系列答案
相关题目
 ,并写出△
,并写出△









 当CE= 时,
当CE= 时, .
.