题目内容
如图二次函数 的图象经过
的图象经过 和
和 两点,且交
两点,且交 轴于点
轴于点 .
.
(1)试确定 、
、 的值;
的值;
(2)过点 作
作 轴交抛物线于点
轴交抛物线于点 点
点 为此抛物线的顶点,试确定
为此抛物线的顶点,试确定 的形状.
的形状.
参考公式:顶点坐标

【答案】
解:(1)将 、
、 两点坐标代入解析式,有:
两点坐标代入解析式,有:
解得:
(2)求出抛物线的顶点

 是等腰直角三角形
是等腰直角三角形
【解析】(1)把A和B两点的坐标代入函数解析式,就可以得到一个关于b,c的方程组,解方程组就可以求出b,c的值.
(2)根据抛物线的顶点坐标的公式代入就可以求出顶点坐标,在抛物线的解析式中,令x=0,解得C点的坐标;C点与D的纵坐标相同,把纵坐标的值代入函数解析式就可以得到D点的坐标,根据坐标就可以求出△CDM的三边的长度.从而判断三角形的形状.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
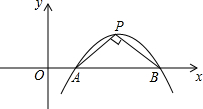 如图所示的抛物线是
如图所示的抛物线是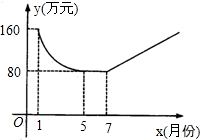 试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.
试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示. 试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.
试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.
 的图象经平移而得到的,此时抛物线过点A(1,0)和x轴上点A右侧的点B,顶点为P.
的图象经平移而得到的,此时抛物线过点A(1,0)和x轴上点A右侧的点B,顶点为P.