题目内容

如图，点A₁、A₂、A₃、A₄，都在线段AF上，且AB=A₁B，A₁C=A₁A₂，A₂D=A₂A₃，A₃E=A₃A₄，若∠B=20°，则∠EA₄A₃=________ 度．

10
分析：根据等腰三角形两底角相等，利用三角形内角和等于180°求出∠AA₁B，再根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和的性质列式进行计算即可得解．
解答：∵∠B=20°，AB=A₁B，
∴∠AA₁B= $\text{[math]}$ （180°-∠B）= $\text{[math]}$ （180°-20°）=80°，
∵A₁C=A₁A₂，
∴∠A₁CA₂=∠CA₂A₁= $\text{[math]}$ ∠AA₁B= $\text{[math]}$ ×80°=40°，
同理可得∠DA₃A₂= $\text{[math]}$ ∠CA₂A₁= $\text{[math]}$ ×40°=20°，
∠EA₄A₃= $\text{[math]}$ ∠DA₃A₂= $\text{[math]}$ ×20°=10°，
故答案为：10．
点评：本题考查了等腰三角形等边对等角的性质，等腰三角形两底角相等的性质，依次求出后一个角是前一个角的一半是解题的关键．

练习册系列答案

上海作业系列答案

海淀名师伴你学同步学练测系列答案

非练不可系列答案

孟建平名校考卷系列答案

新课标三习五练课堂作业系列答案

金牌教练系列答案

跟我学系列答案

精考卷全程测试系列答案

名师点津系列答案

零失误分层训练系列答案

相关题目

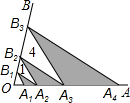如图，点A₁，A₂，A₃，A₄在射线OA上，点B₁，B₂，B₃在射线OB上，且A₁B₁∥A₂B₂∥A₃B₃，A₂B₁∥A₃B₂∥A₄B₃．若△A₂B₁B₂，△A₃B₂B₃的面积分别为1，4，则图中三个阴影三角形面积之和为

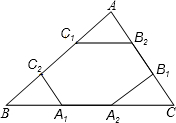如图，点A₁、A₂，B₁、B₂，C₁、C₂分别是△ABC的边BC、CA、AB的三等分点，若△ABC的周长为L，则六边形A₁A₂B₁B₂C₁C₂的周长为（　　）

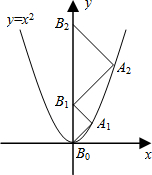如图，点A₁、A₂、A₃、…、A_n在抛物线y=x²图象点B₁、B₂、B₃、…、B_n在y轴上，若△A₁B₀B₁、△A₂B₁B₂、…、△A_nB_n-1B_n都为等腰直角三角形（点B₀是坐标原点），则△A₂₀₁₂B₂₀₁₁B₂₀₁₂的腰长=

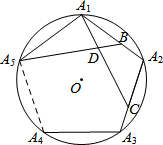如图，点A₁、A₂、A₃、…、A_n在抛物线y=x²图象上，点B₁、B₂、B₃、…、B_n在y轴上，若△A₁B₀B₁、△A₂B₁B₂、…、△A_nB_n-1B_n都为等腰直角三角形（点B₀是坐标原点），则△A₂₀₁₃B₂₀₁₂B₂₀₁₃的腰长=

（2013•南京二模）如图，点A₁、A₂、A₃、A₄、A₅在⊙O上，且

，B、C分别是A₁A₂、A₂A₃上两点，A₁B=A₂C，A₅B与A₁C相交于点D，则∠A₅DC的度数为