Question

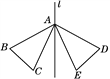
【题目】如图，四边形是矩形，点在线段的延长线上，连接交于点，，点是的中点．

（）求证：．

（）若，，，点是的中点，求的长．

Answer 1

【答案】（）见解析（）

【解析】试题分析：

（1）由已知条件易证∠GAD=∠ADE=∠CED，结合∠AGE=∠GAD+∠ADE，可得∠AGE=2∠CED，再结合∠AED=2∠CED即可得到∠AGE=∠AED，从而可得AE=AG；

（2）如下图，连接GH，由（1）中结论可知AE=AG=，结合BE=2，在Rt△ABE中可求得AB=11，结合BF=1可求得AF=10，再结合G是DF的中点，H是AD的中点由三角形中位线定理即可求得GH=5.

试题解析：

（）∵ 四边形是矩形，

∴ ，，

∴ ，

又∵ 为中点，

∴ ，

∴ ，

∵∠AGE=∠GAD+∠ADE，

∴ ，

又∵ ，

∴ ，

．

（）连接，由（）知：=，

在中，，，

∴ ，

∵ ，

∴ ，

∵ 是中点，是中点，

∴ ．