题目内容
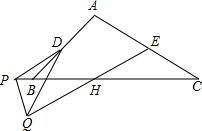 如图,在△ABC和△PQD中,
如图,在△ABC和△PQD中,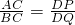 ,∠C=∠PDQ,D、E分别是AB、AC的中点,点P在直线BC上,联结EQ,交PC于点H.猜想线段EH与AC之间的数量关系,并证明你的结论.
,∠C=∠PDQ,D、E分别是AB、AC的中点,点P在直线BC上,联结EQ,交PC于点H.猜想线段EH与AC之间的数量关系,并证明你的结论.
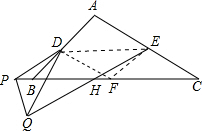 猜想:
猜想: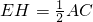 .
.证明:取BC边的中点F,连接DE、DF.
∵D、E、F分别是AB、AC、BC的中点,
∴DE∥BC且
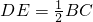 ,DF∥AC且
,DF∥AC且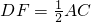 .
.∴四边形DFCE是平行四边形.
∴∠C=∠EDF,
∵∠C=∠PDQ,
∴∠PDQ=∠EDF,
∴∠PDF=∠QDE.
又∵
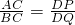 ,
,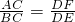 ,
,∴
 .
.∴△PDF∽△QDE.
∴∠DEQ=∠DFP.
又∵DE∥BC,DF∥AC,
∴∠DEQ=∠EHC,∠DFP=∠C.
∴∠C=∠EHC.
∴EH=EC.
∴
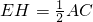 .
.分析:取BC边的中点F,连接DE、DF,利用三角形中位线的性质得出四边形DFCE是平行四边形,进而得出△PDF∽△QDE,即可得出EH与AC之间的数量关系.
点评:此题主要考查了平行四边形的判定以及三角形中位线的性质和相似三角形的判定与性质等知识,得出△PDF∽△QDE是解题关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 22、已知,如图,在△ABC和△EDB中,∠ACB=∠EBD=90°,点E在BC上,DE⊥AB交AB于F,且AB=ED.求证:DB=BC.
22、已知,如图,在△ABC和△EDB中,∠ACB=∠EBD=90°,点E在BC上,DE⊥AB交AB于F,且AB=ED.求证:DB=BC. 如图,在△ABC和△DEF中,AC∥DE,∠EFD与∠B互补,DE=mAC(m>1).试探索线段EF与AB的数量关系,并证明你的结论.
如图,在△ABC和△DEF中,AC∥DE,∠EFD与∠B互补,DE=mAC(m>1).试探索线段EF与AB的数量关系,并证明你的结论. 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件
如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件 如图,在△ABC和△ABD中,AC⊥BC,AD⊥BD,E是AB边上的中点.则DE
如图,在△ABC和△ABD中,AC⊥BC,AD⊥BD,E是AB边上的中点.则DE 如图,在△ABC和△DEF中,∠A=∠D,∠C=∠F,AC=DF,请说明AE=BD的理由.
如图,在△ABC和△DEF中,∠A=∠D,∠C=∠F,AC=DF,请说明AE=BD的理由.