题目内容
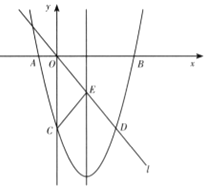
【题目】如图，已知在平面直角坐标系xOy中，抛物线y=
与y轴交于点A，顶点为B，直线l：y=-
x+b经过点A，与抛物线的对称轴交于点C，点P是对称轴上的一个动点，若AP+
PC的值最小，则点P的坐标为（ ）
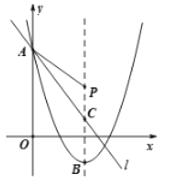
A. （3，1）
B. （3，
）
C. （3，
）
D. （3，
）
【答案】B
【解析】
如图，过点C作CD⊥y轴于D，作点A关于抛物线对称轴的对称点A’，连接AA’，CA’，过点A作AE⊥CA’交抛物线对称轴于点P，此时点A到A’C距离最小.可求得AP+
PC= AP+PE，当A、P、E三点共线时AP+PC最小，故可求得结果.
如图，过点C作CD⊥y轴于D，作点A关于抛物线对称轴的对称点A’，连接AA’，CA’，过点A作AE⊥CA’交抛物线对称轴于点P，此时点A到A’C距离最小。
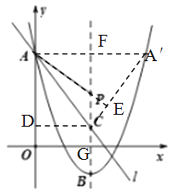
∵抛物线y=
∴A（0，5），A’（6，5）
∵直线l：y=-
x+b
∴C（3，1），D（0，1）
∵∠ACP=∠ECP
∴Sin∠ECP=Sin∠ACP=
∴AP+PC=AP+Sin∠ECP·PC=AP+PE
∴当A、P、E三点共线时AP+PC最小
∴∠A’AP=∠ECP=∠ACP
∴PF=AF·tan∠FAP=
∴P（3，
）
故选B.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
