题目内容
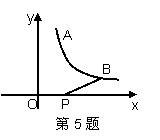
如图,已知:AB为⊙O的直径,C为⊙O上一点, F为 的中点,过F作DE∥BC交AB的延长线于D,交AC的延长线于E.
F为 的中点,过F作DE∥BC交AB的延长线于D,交AC的延长线于E.
 (1)求证:DE为⊙O的切线;
(1)求证:DE为⊙O的切线;
(2)若⊙O的半径为10,∠A=45°,求阴影部分的面积.
 |
(1)  证明:连接OF,OC,作OG⊥AC,垂足为G----------------------------1
证明:连接OF,OC,作OG⊥AC,垂足为G----------------------------1
 ∵F为 的
∵F为 的 中点
中点
∴
∴∠1=∠2---------------------------------------------------------------------2
∵OB=OC
∴OF⊥BC-------------------------------------------------------4
∴∠ONC=90°
∵DE∥BC
∴∠OFE=∠ONC=90°
∴OF⊥DE---------------------------------------------------5
∴DE为⊙O的切线---------------------------------------------------------------------6
(2)∵OG⊥AC
∴AG=CG=5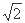 -------------------------------------------------------7
-------------------------------------------------------7
AE=AG+GE=AG+OF=5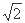 +10--
+10-- --------------------------------------------------8
--------------------------------------------------8
∵AB为⊙O的直径
∴∠ACB=90°
∵DE∥BC
∴∠E=∠ACB=90°
∵∠A=45°
∴DE=AE=5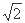 +10----------------------------------------------------------------9
+10----------------------------------------------------------------9
∵∠BOC=2∠A=90°----------------- ----------------------------
---------------------------- -----------------------10
-----------------------10
∴S阴影部分=S△ADE-S△AOC-S扇形OBC

= --------------12

某政府部门招聘公务员 1 人,对前来应聘的 A,B,C 三人进行了三项测试.他们的各项测试成 绩如下表所示:
| 测试项目 | 测试成绩 | ||
| A | B | C | |
| 笔 试 | 90 | 80 | 75 |
| 面 试 | 85 | 85 | 85 |
| 群众评议 | 77 | 84 | 80 |
根据三项测试的平均成绩确定录用人选,那么谁将被录用?
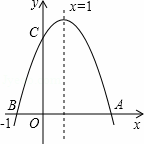
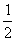 ,y1),B(2,y2)为反比例函数
,y1),B(2,y2)为反比例函数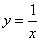 图像上的两点,动点P(x,0)
图像上的两点,动点P(x,0)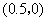 B.
B. C.
C. D.
D.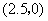
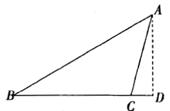
 中,
中, ,过点
,过点 作
作 ,垂足为
,垂足为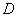 ,
,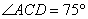 .
.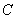 到
到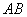 的距离;
的距离;  (2)求线段
(2)求线段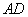 的长度.
的长度.
 -
-
 在实数
在实数  ,0,﹣ ,506,π,0.1
,0,﹣ ,506,π,0.1  中,无理数的个数是( )
中,无理数的个数是( ) B.
B.  C.
C.  D.
D.
