题目内容
解不等式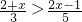 的过程中,错误之处是
的过程中,错误之处是
- A.5(2+x)>3(2x-1)
- B.10+5x>6x-3
- C.5x-6x>-3-10
- D.x>13
D
分析:系数化为1的过程中,不等式两边同时除以-1,依据不等式的性质:在不等式的两边同时乘以或除以同一个负数不等号的方向改变.
解答:解不等式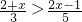 ,
,
不等式两边同时乘以15得:5(2+x)>3(2x-1),
去括号得:10+5x>6x-3,
移项得:5x-6x>-3-10,
合并同类项得:-x>-13,
系数化1得:x<13;
所以,D错误;
故本题选D.
点评:解不等式依据不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.特别是在系数化为1这一个过程中要注意不等号的方向的变化.
分析:系数化为1的过程中,不等式两边同时除以-1,依据不等式的性质:在不等式的两边同时乘以或除以同一个负数不等号的方向改变.
解答:解不等式
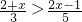 ,
,不等式两边同时乘以15得:5(2+x)>3(2x-1),
去括号得:10+5x>6x-3,
移项得:5x-6x>-3-10,
合并同类项得:-x>-13,
系数化1得:x<13;
所以,D错误;
故本题选D.
点评:解不等式依据不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.特别是在系数化为1这一个过程中要注意不等号的方向的变化.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
解不等式
>
的过程中,错误之处是( )
| 2+x |
| 3 |
| 2x-1 |
| 5 |
| A、5(2+x)>3(2x-1) |
| B、10+5x>6x-3 |
| C、5x-6x>-3-10 |
| D、x>13 |