题目内容
 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E是
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E是
- A.45°
- B.22.5°
- C.11.5°
- D.40°
B
分析:连接BD,根据正方形的性质求出∠ABD=45°,AC=BD=BE,推出∠E=∠BDE,根据三角形的外角性质求出即可.
解答:连接BD,
∵正方形ABCD,
∴AC=BD,∠ABC=90°,
∴∠ABD= ∠ABC=45°,
∠ABC=45°,
∵BE=AC,AC=BD,
∴BD=BE,
∴∠E=∠BDE,
∵∠E+∠BDE=∠ABD=45°,
∴∠E=22.5°.
故选B.
点评:本题主要考查对正方形的性质,三角形的外角性质,等腰三角形的性质等知识点的连接和掌握,能求出∠E=∠BDE和∠ABD的度数是解此题的关键.
分析:连接BD,根据正方形的性质求出∠ABD=45°,AC=BD=BE,推出∠E=∠BDE,根据三角形的外角性质求出即可.
解答:连接BD,

∵正方形ABCD,
∴AC=BD,∠ABC=90°,
∴∠ABD=
 ∠ABC=45°,
∠ABC=45°,∵BE=AC,AC=BD,
∴BD=BE,
∴∠E=∠BDE,
∵∠E+∠BDE=∠ABD=45°,
∴∠E=22.5°.
故选B.
点评:本题主要考查对正方形的性质,三角形的外角性质,等腰三角形的性质等知识点的连接和掌握,能求出∠E=∠BDE和∠ABD的度数是解此题的关键.

练习册系列答案
相关题目
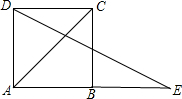 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E是( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E是( )| A、45° | B、22.5° | C、11.5° | D、40° |
 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=

