题目内容
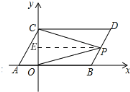
【题目】如图![]() ,在平面直角坐标系中,点
,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将线段
,将线段![]() 先向上平移
先向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到线段
个单位长度,得到线段![]() ,连接
,连接![]() ,
,![]() ,构成平行四边形
,构成平行四边形![]() .
.
(1)请写出点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上任意一个点(不与
上任意一个点(不与![]() 、
、![]() 重合),连接
重合),连接![]() 、
、![]() ,试探索
,试探索![]() 、
、![]() 、
、![]() 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.

【答案】(1)8;(2)![]() 或
或![]() (3)
(3)![]()
【解析】
(1)根据平移直接得到点C,D坐标,用面积公式计算;
(2)设出Q的坐标,OQ=|m|,用![]() =
=![]() 建立方程,解方程即可;
建立方程,解方程即可;
(3)作出辅助线,平行线,根据两直线平行,内错角相等,求解即可.
解:(1)∵ 线段![]() 先向上平移
先向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到线段
个单位长度,得到线段![]() ,
,
且![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() ;
;
(2)∵点![]() 在
在![]() 轴上,设
轴上,设![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() .
.
(3)如图,
∵ 线段![]() 是线段
是线段![]() 平移得到,
平移得到,
∴![]() ,
,
作![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目