Question

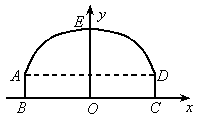
(2005　湖北武汉)如图所示，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系．y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．

(1)求抛物线的解析式；

(2)如果该隧道内设双行道，现有一辆货运卡车高4.2m，宽2.4m，这辆货运卡车能否通过该隧道？过计算说明你的结论．

Answer 1

答案：略
解析：

解　(1)由题设该抛物线方程为，又A(－4，2)，D(4，2)，E(0，6)在抛物线上， ∴ 解得 ∴抛物线的解析式为． (2)取x=2.4，解得y=4.56＞4.2，能通过．

提示：

点评　要求抛物线的解析式，需确定出任意三点的坐标，或顶点坐标或对称轴或最值．此题是一道实际生活题，注意题设条件．