题目内容
如图，O是正方形ABCD的对角线BD上一点，半径为1的⊙O与边AB、BC都相切，现将点D翻折到点O，折痕EF恰与⊙O相切，则正方形ABCD的边长是
- A.2
- B.3
- C.
- D.
D
分析：延长FO交AB于点G，根据折叠对称可以知道OF⊥CD，所以OG⊥AB，即点G是切点，OD交EF于点H，点H是切点．结合图形可知OG=OH=HD=EH=1，易求得DE的长，然后求出正方形的边长．
解答：
解：如图：延长FO交AB于点G，则点G是切点，设OD交EF于点H，则点H是切点，
∵四边形ABCD是正方形，点O在对角线BD上，
∴DF=DE，OF⊥DC，
∴GF⊥DC，
∴OG⊥AB，
∴OG=OH=HD=HE=AE=1．
在等腰直角三角形DEH中，OD=2OH=2，
∴DE=OE=
OD=，
∴AD=AE+DE=1+．
即正方形ABCD的边长是：1+．
故选D．
点评：此题考查了切线的性质、正方形的性质以及折叠的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．
分析：延长FO交AB于点G，根据折叠对称可以知道OF⊥CD，所以OG⊥AB，即点G是切点，OD交EF于点H，点H是切点．结合图形可知OG=OH=HD=EH=1，易求得DE的长，然后求出正方形的边长．
解答：
解：如图：延长FO交AB于点G，则点G是切点，设OD交EF于点H，则点H是切点，∵四边形ABCD是正方形，点O在对角线BD上，
∴DF=DE，OF⊥DC，
∴GF⊥DC，
∴OG⊥AB，
∴OG=OH=HD=HE=AE=1．
在等腰直角三角形DEH中，OD=2OH=2，
∴DE=OE=
OD=，∴AD=AE+DE=1+
．即正方形ABCD的边长是：1+
．故选D．
点评：此题考查了切线的性质、正方形的性质以及折叠的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
如图，E是正方形ABCD对角线AC上一点，EF⊥AB，EG⊥BC，F、G是垂足，若正方形ABCD周长为a，则EF+EG等于（ ）A、
| ||
B、
| ||
| C、a | ||
| D、2a |
22、如图，ABCD是正方形，P是对角线BD上一点，过P点作直线EF、GH分别平行于AB、BC，交两组对边于E、F、G、H，则四边形PEDG，四边形PHBF都是正方形，四边形PEAH、四边形PGCF都是矩形，设正方形PEDG的边长是a，正方形PHBF的边长是b． 请动手实践并得出结论：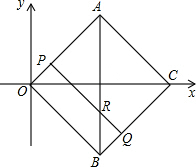
，两点运动到相遇停止．设△OPQ的面积为S．请求出S关于t的函数关系式以及自变量t的取值范围．
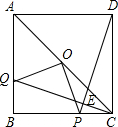点P，连接OP，OQ；