题目内容
若关于x的方程 =-1的解为正数,则a的取值范围是 .
=-1的解为正数,则a的取值范围是 .
【答案】分析:先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求a的取值范围.
解答:解:去分母得,2x+a=-x+2
解得x=
∵分母x-2≠0即x≠2
∴ ≠2
≠2
解得,a≠-4
又∵x>0
∴
解得,a<2
则a的取值范围是a<2且a≠-4.
点评:本题考查了分式方程无解的条件,是需要识记的内容.并且在解方程去分母的过程中,一定要注意分数线起到括号的作用,并且要注意没有分母的项不要漏乘.
解答:解:去分母得,2x+a=-x+2
解得x=

∵分母x-2≠0即x≠2
∴
 ≠2
≠2解得,a≠-4
又∵x>0
∴

解得,a<2
则a的取值范围是a<2且a≠-4.
点评:本题考查了分式方程无解的条件,是需要识记的内容.并且在解方程去分母的过程中,一定要注意分数线起到括号的作用,并且要注意没有分母的项不要漏乘.

练习册系列答案
相关题目
若关于x的方程(x-2)+3k=
的根是负数,则k的取值范围是( )
| x+k |
| 3 |
A、k>
| ||
B、k≥
| ||
C、k<
| ||
D、k≤
|
若关于x的方程(m-1)xm2+1+5x+2=0是一元二次方程,则m的值等于( )
| A、1 | B、-1 | C、±1 | D、0 |
若关于x的方程3x+a=0的解比方程-
x-4=0的解大2,则a的值( )
| 2 |
| 3 |
| A、-18 | B、12 |
| C、24 | D、-12 |
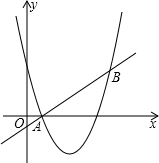 直线y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,且不等式x+a>x2+bx+c 的整数解为K,若关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),求m的值.
直线y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,且不等式x+a>x2+bx+c 的整数解为K,若关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),求m的值.