题目内容
10．
如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，则cos∠A=$\frac{4}{5}$．
分析 根据勾股定理，可得AB的长，根据余弦是邻边比斜边，可得答案．
解答 解：由勾股定理，得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5，
cos∠A=$\frac{AC}{AB}$=$\frac{4}{5}$，
故答案为：$\frac{4}{5}$．
点评 本题考查了锐角三角函数的定义，利用余弦是邻边比斜边是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
20．
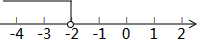如图，关于x的一元一次不等式ax-2＞0的解集在数轴上表示如图，则关于y的方程ay+2=0的解为（ ）
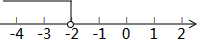如图，关于x的一元一次不等式ax-2＞0的解集在数轴上表示如图，则关于y的方程ay+2=0的解为（ ）| A． | y=-2 | B． | y=2 | C． | y=-1 | D． | y=1 |
如图，若在象棋棋盘上建立直角坐标系，使“帅”位于点（-3，-2），“炮”位于点（-2，0），则“兵”位于的点的坐标为（-5，1）．
5．下列运算正确的是（ ）
| A． | （a2）3=a5 | B． | a+2a=3a2 | C． | a6•a3=a9 | D． | （a-b）2=a2-b2 |
15．下列各式计算正确的是（ ）
| A． | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | B． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | C． | x3•x5=x15 | D． | x11÷x6=x5 |
已知下列命题为真命题的是①②④（只填序号）．
20．
如图，D为等边三角形ABC内的一点，DA=5，DB=4，DC=3，将线段AD以点A为旋转中心逆时针旋转60°，得到线段AD′，连接DD′，则tan∠DD′C=（ ）
如图，D为等边三角形ABC内的一点，DA=5，DB=4，DC=3，将线段AD以点A为旋转中心逆时针旋转60°，得到线段AD′，连接DD′，则tan∠DD′C=（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{5}{4}$ | D． | $\frac{4}{5}$ |