题目内容
 如图,△ABC是正三角形,AB=4cm,D,E,F分别是AB,BC,CA边上的动点,且AD=BE=CF.
如图,△ABC是正三角形,AB=4cm,D,E,F分别是AB,BC,CA边上的动点,且AD=BE=CF.
(1)试说明:△DEF是正三角形;
(2)当DF⊥AC时,求AD的长;
(3)当△DEF的面积为 cm2时,求AD的长.
cm2时,求AD的长.
(1)证明:∵△ABC是正三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°;
由AD=BE=CF可得出:BD=AF=CE,
∴△ADF≌△BED≌△CFE(SAS),
∴DE=EF=DF
∴△DEF是正三角形,
(2)解:设AF=x,在Rt△ADF中,∠A=60°,
∴∠ADF=30°,
∴AD=2AF=2x,
又∵AF+CF=AC
∴3x=4,x= ,即AD=
,即AD= ,
,
(3)解:作DM⊥EF于点M,过D作DN⊥AC于N,设AD=x,
∵∠A=60°,
∴∠ADN=30°,
∴AN= x,DN=
x,DN= x,
x,
则NF=4-x- x=4-
x=4- x,
x,

当△DEF的面积为 cm2时,
cm2时,
有面积公式: =
= DE•DM=
DE•DM= DE•DFsin60°,
DE•DFsin60°,
又∵DE=DF,
∴解得DE=2=DF,
在Rt△DFN中,由勾股定理得:22=( x)2+(4-
x)2+(4- x)2
x)2
x=2,
∴AD=2.
故AD=2.
分析:(1)要证明△DEF是正三角形,则需证明三边相等,由边角边定理可得△ADF≌△BED≌△CFE,由此可得本题结论;
(2)设AF=x,在Rt△ADF中,∠A=60°,可得∠ADF=30°,从而AD=2AF=2x,将其代入AF+CF=AC即可求得AD的长;
(3)由△DEF的面积为 cm2时,有面积公式:
cm2时,有面积公式: =
= DE•DFsin60°,根据DE=DF,可得DE=2,设AD=x,则FN=4-
DE•DFsin60°,根据DE=DF,可得DE=2,设AD=x,则FN=4- x,DN=
x,DN= x,根据勾股定理求出x即可.
x,根据勾股定理求出x即可.
点评:本题考查了等边三角形的性质,难度适中,关键掌握等边三角形的判定与性质及面积公式.
∴AB=BC=AC,∠A=∠B=∠C=60°;
由AD=BE=CF可得出:BD=AF=CE,
∴△ADF≌△BED≌△CFE(SAS),
∴DE=EF=DF
∴△DEF是正三角形,
(2)解:设AF=x,在Rt△ADF中,∠A=60°,
∴∠ADF=30°,
∴AD=2AF=2x,
又∵AF+CF=AC
∴3x=4,x=
 ,即AD=
,即AD= ,
,(3)解:作DM⊥EF于点M,过D作DN⊥AC于N,设AD=x,
∵∠A=60°,
∴∠ADN=30°,
∴AN=
 x,DN=
x,DN= x,
x,则NF=4-x-
 x=4-
x=4- x,
x,
当△DEF的面积为
 cm2时,
cm2时,有面积公式:
 =
= DE•DM=
DE•DM= DE•DFsin60°,
DE•DFsin60°,又∵DE=DF,
∴解得DE=2=DF,
在Rt△DFN中,由勾股定理得:22=(
 x)2+(4-
x)2+(4- x)2
x)2x=2,
∴AD=2.
故AD=2.
分析:(1)要证明△DEF是正三角形,则需证明三边相等,由边角边定理可得△ADF≌△BED≌△CFE,由此可得本题结论;
(2)设AF=x,在Rt△ADF中,∠A=60°,可得∠ADF=30°,从而AD=2AF=2x,将其代入AF+CF=AC即可求得AD的长;
(3)由△DEF的面积为
 cm2时,有面积公式:
cm2时,有面积公式: =
= DE•DFsin60°,根据DE=DF,可得DE=2,设AD=x,则FN=4-
DE•DFsin60°,根据DE=DF,可得DE=2,设AD=x,则FN=4- x,DN=
x,DN= x,根据勾股定理求出x即可.
x,根据勾股定理求出x即可.点评:本题考查了等边三角形的性质,难度适中,关键掌握等边三角形的判定与性质及面积公式.

练习册系列答案
相关题目
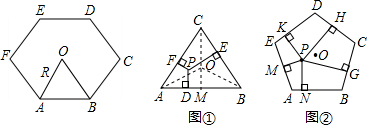 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
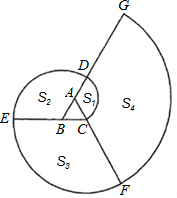 依次为A、B、C….当渐开线延伸开时,形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1.
依次为A、B、C….当渐开线延伸开时,形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1.
 如图,△ABC是一个电子跳蚤游戏盘,其中AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第一次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第二次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第三次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P1与P2014之间的距离为( )
如图,△ABC是一个电子跳蚤游戏盘,其中AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第一次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第二次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第三次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P1与P2014之间的距离为( ) 的圆心依次为A、B、C….当渐开线延伸开时,形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1.
的圆心依次为A、B、C….当渐开线延伸开时,形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1.