题目内容
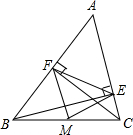如图，BE、CF分别是△ABC的高，M为BC的中点，EF=5，BC=8，则△EFM的周长是________．
13
分析：根据直角三角形斜边上的中线等于斜边的一半，先求出EM=FM=
BC，再求△EFM的周长就不难了．
解答：∵BE、CF分别是△ABC的高，M为BC的中点，BC=8，
∴在Rt△BCE中，EM=BC=4，
在Rt△BCF中，FM=BC=4，
又∵EF=5，
∴△EFM的周长=EM+FM+EF=4+4+5=13．
点评：本题主要利用直角三角形斜边上的中线等于斜边的一半的性质．
分析：根据直角三角形斜边上的中线等于斜边的一半，先求出EM=FM=
BC，再求△EFM的周长就不难了．解答：∵BE、CF分别是△ABC的高，M为BC的中点，BC=8，
∴在Rt△BCE中，EM=
BC=4，在Rt△BCF中，FM=
BC=4，又∵EF=5，
∴△EFM的周长=EM+FM+EF=4+4+5=13．
点评：本题主要利用直角三角形斜边上的中线等于斜边的一半的性质．
练习册系列答案
相关题目
