题目内容
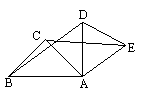
如图所示，将等边△ABC绕点A旋转∠BAD的度数之后得到等边△ADE，连BD，CE．试问△BAD与△CAE能全等吗？请说明理由．
答案：
解析：
提示：
解析：
|
答案：△BAD与△CAE是全等的．理由：因为△ABC为等边三角形，故AB＝BC＝AC．而△DAE是由△ABC绕点A旋转而成的，由旋转图形的性质可以知道：AD＝AB，AE＝AC，且∠BAD＝∠CAE，因而△BAD≌△CAE(SAS)． 剖析：旋转、翻折、平移图形必是全等图形，故问题得以解决． |
提示：
|
方法提炼： 1．由旋转图形特征可知，∠BAD＝∠CAE，且AB＝AD，AC＝AE，又AB＝BC＝AC，从而可以利用SAS得到△BAD≌△CAE． 2．旋转图形的性质是解答本题的关键．事实上，本题的条件可以弱一些，只需△ABC为等腰三角形，即AB＝AC即可．同学们不妨试试看． |
练习册系列答案
相关题目
，D、E分别是AB、AC上的点，
，如图（1），然后将
绕A点顺时针旋转
，使B、A、E三点在同一直线上，得到图（2），M、N分别是BD、CE的中点，连接AM、AN、MN得到图（3），请解答下列问题：
与
，D、E分别是AB、AC上的点，
，如图（1），然后将
绕A点顺时针旋转
，使B、A、E三点在同一直线上，得到图（2），M、N分别是BD、CE的中点，连接AM、AN、MN得到图（3），请解答下列问题：
与
