题目内容
12、一元二次方程x2-2x+k=0有实根,则k的取值范围是
k≤1
;若它有一根为2,则另一根是0
.分析:(1)由一元二次方程x2-2x+k=0有实根,得△≥0,即△=4-4k≥0,解不等式得到k的取值范围;
(2)把x=2代入原方程,得4-4+k=0,解得k=0,然后把k=0代入原方程,解方程可得到另一根.
(2)把x=2代入原方程,得4-4+k=0,解得k=0,然后把k=0代入原方程,解方程可得到另一根.
解答:解:∵一元二次方程x2-2x+k=0有实根,
∴△≥0,即△=4-4k≥0,解得k≤1.
所以k的取值范围是k≤1.
∵当方程有一根为2
∴把x=2代入原方程,得4-4+k=0,解得k=0,
原方程变为:x2-2x=0,解得x1=2,x2=0.
所以若它有一根为2,则另一根是0.
故答案为k≤1;0.
∴△≥0,即△=4-4k≥0,解得k≤1.
所以k的取值范围是k≤1.
∵当方程有一根为2
∴把x=2代入原方程,得4-4+k=0,解得k=0,
原方程变为:x2-2x=0,解得x1=2,x2=0.
所以若它有一根为2,则另一根是0.
故答案为k≤1;0.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元二次方程的解法.

练习册系列答案
相关题目
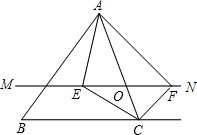 从甲、乙两题中选做一题,如果两题都做,只以甲题计分.
从甲、乙两题中选做一题,如果两题都做,只以甲题计分.