题目内容
【题目】如图，一次函数y=﹣x+5的图象与反比例函数y= 
（k≠0）在第一象限的图象交于A（1，n）和B两点．
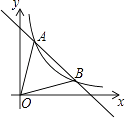
（1）求反比例函数的解析式与点B坐标；
（2）求△AOB的面积；
（3）在第一象限内，当一次函数y=﹣x+5的值小于反比例函数y= （k≠0）的值时，写出自变量x的取值范围．
【答案】
（1）解：∵一次函数y=﹣x+5的图象过点A（1，n），
∴n=﹣1+5，解得：n=4，
∴点A的坐标为（1，4）．
∵反比例函数y= 
（k≠0）过点A（1，4），
∴k=1×4=4，
∴反比例函数的解析式为y= 
．
联立 
，解得： 
或 
，
∴点B的坐标为（4，1）
（2）解：延长AB交x轴与点C，则C（5，0），如图所示．
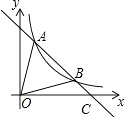
∵A（1，4），B（4，1），
∴S△AOB=S△AOC﹣S△BOC= 
OCyA﹣ OCyB=10﹣ 
= 
（3）解：观察函数图象，发现：
当0＜x＜1或x＞4时，反比例函数图象在一次函数图象上方，
∴当一次函数y=﹣x+5的值小于反比例函数y= （k≠0）的值时，x的取值范围为0＜x＜1或x＞4
【解析】（1）由一次函数y=﹣x+5的图象过点A（1，n），求出点A的坐标，得到反比例函数的解析式，求出点B的坐标；（2）直线AB交x轴与点C，得到C（5，0），求出S△AOB=S△AOC﹣S△BOC的面积；（3）观察函数图象，当0＜x＜1或x＞4时，反比例函数图象在一次函数图象上方，得到一次函数的值小于反比例函数的值时，x的取值范围.
【题目】父亲告诉小明：“距离地面越高，温度越低，”并给小明出示了下面的表格。
距离地面高度（千米） | 0 | 1 | 2 | 3 | 4 | 5 |
温度（℃） | 20 | 14 | 8 | 2 |
|
|
根据上表，父亲还给小明出了下面几个问题，你和小明一起回答。
（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）如果用h表示距离地面的高度，用t表示温度，那么随着h的变化，t是怎么变化的？
（3）你能猜出距离地面6千米的高空温度是多少吗？
