题目内容
正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时Rt△ABM ∽Rt△AMN,求此时x的值.

(1)证明:∵四边形ABCD是正方形,∴∠B=∠C=90°,∠ABM+∠BAM=90°
∵∠ABM+∠CMN+∠AMN=180°,∠AMN=90°∴∠AMB+∠CMN=90°∴∠BAM=∠CMN
∴Rt△ABM∽Rt△MCN
(2)∵Rt△ABM∽Rt△MCN,∴![]() 即
即![]() 解得:
解得:![]()
∵![]() ∴
∴![]() ,
,
即:![]()
又∵![]()
∴当x=2时,y有最大值10.
∴当M点运动到BC的中点时,四边形ABCN的面积最大,最大面积是10.
(3)∵Rt△ABM∽Rt△MCN,∴![]() ,即
,即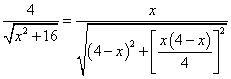
化简得:![]() ,解得:x=2
,解得:x=2
∴当M点运动到BC的中点时Rt△ABM ∽Rt△AMN,此时x的值为2.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
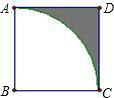 如图,正方形ABCD边长为2cm,以点B为圆心,AB的长为半径作弧
如图,正方形ABCD边长为2cm,以点B为圆心,AB的长为半径作弧 |
| AC |
| A、(4-π)cm2 |
| B、(8-π)cm2 |
| C、(2π-4)cm2 |
| D、(π-2)cm2 |
 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直. 如图所示,正方形ABCD边长为2,点E在CB的延长线上,BD=BE,则tan∠BAE的值为
如图所示,正方形ABCD边长为2,点E在CB的延长线上,BD=BE,则tan∠BAE的值为 s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,