题目内容
在平面直角坐标系中,反比例函数y=
(k≠0)与y=
的图象关于x轴对称,又与直线y=ax+2必有交点,试确定a的取值范围.
| k |
| x |
| 3 |
| x |
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:根据反比例函数的性质和关于x轴对称的特征得到反比例函数y=
(k≠0)的解析式为y=-
,再利用反比例函数与一次函数的交点问题得到方程组
,消去y得ax2+2x+3=0,然后讨论:当a=0时,2x+3=0,解得x=-
,满足条件;当a≠0,△=22-4a•3≥0,解得a≤
且a≠0,然后综合两种情况即可得到a的范围.
| k |
| x |
| 3 |
| x |
|
| 3 |
| 2 |
| 1 |
| 3 |
解答:解:∵反比例函数y=
(k≠0)与y=
的图象关于x轴对称,
∴反比例函数y=
(k≠0)的解析式为y=-
,
由方程组
得ax2+2x+3=0,
当a=0时,2x+3=0,解得x=-
;
当a≠0,△=22-4a•3≥0,解得a≤
,即a≤
且a≠0,
∴a的取值范围为a≤
.
| k |
| x |
| 3 |
| x |
∴反比例函数y=
| k |
| x |
| 3 |
| x |
由方程组
|
当a=0时,2x+3=0,解得x=-
| 3 |
| 2 |
当a≠0,△=22-4a•3≥0,解得a≤
| 1 |
| 3 |
| 1 |
| 3 |
∴a的取值范围为a≤
| 1 |
| 3 |
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
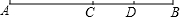 如图,C是AB的中点,D是BC的中点,下列说法不正确的是( )
如图,C是AB的中点,D是BC的中点,下列说法不正确的是( )| A、若AC=4,则DB=2 |
| B、若CD=3,则AC=6 |
| C、若AB=8,则CD=2 |
| D、若CD=1,则AD=4 |
 已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若
已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若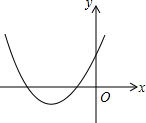 已知二次函数y=ax2+bx+c的图象如图所示,则
已知二次函数y=ax2+bx+c的图象如图所示,则 a、b在数轴上对应的点如图所示:
a、b在数轴上对应的点如图所示: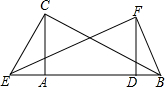 已知,如图,点E,A,D,B在同一条直线上,AC⊥EB,FD⊥EB,CA=FD,CE=FB.求证:BC=EF.
已知,如图,点E,A,D,B在同一条直线上,AC⊥EB,FD⊥EB,CA=FD,CE=FB.求证:BC=EF.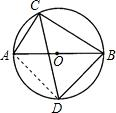 如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是
如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是