��Ŀ����
��֪����x��һԪ���η���x2 (2k+3)x+k2+3k+2=0
(2k+3)x+k2+3k+2=0
��1�����ж��������̸��������
��2�������������̵�������Ϊ�����ꡢ������ĵ�ǡ�ڷ��������� ��ͼ���ϣ�������������m����Сֵ��
��ͼ���ϣ�������������m����Сֵ��
��3����֪��ABC������AB��AC�ij��ǹ����������̵�����ʵ������BC�ij�Ϊ5��
�ٵ�kΪ��ֵʱ����ABC����BCΪб�ߵ�ֱ��������?
�ڵ�kΪ��ֵʱ����ABC�ǵ���������?�������ʱ��ABC���ܳ���
 (2k+3)x+k2+3k+2=0
(2k+3)x+k2+3k+2=0��1�����ж��������̸��������
��2�������������̵�������Ϊ�����ꡢ������ĵ�ǡ�ڷ���������
 ��ͼ���ϣ�������������m����Сֵ��
��ͼ���ϣ�������������m����Сֵ����3����֪��ABC������AB��AC�ij��ǹ����������̵�����ʵ������BC�ij�Ϊ5��
�ٵ�kΪ��ֵʱ����ABC����BCΪб�ߵ�ֱ��������?
�ڵ�kΪ��ֵʱ����ABC�ǵ���������?�������ʱ��ABC���ܳ���
��1������������ȵ�ʵ��������2�� ����3����2��3����k=3��4���ܳ�Ϊ14��16
����3����2��3����k=3��4���ܳ�Ϊ14��16
 ����3����2��3����k=3��4���ܳ�Ϊ14��16
����3����2��3����k=3��4���ܳ�Ϊ14��16�����������1������������ø����б�ʽ��
 ��ֵ�����������жϣ�
��ֵ�����������жϣ���2���跽��x2
 (2k+3)x+k2+3k+2=0��������Ϊ
(2k+3)x+k2+3k+2=0��������Ϊ ��
�� �����������
����������� ������һԪ���η��̸���ϵ���Ĺ�ϵ�ã�
������һԪ���η��̸���ϵ���Ĺ�ϵ�ã� ���Ӷ��ɵ�
���Ӷ��ɵ� ���ٸ��ݶ��κ��������ʼ�����ý����
���ٸ��ݶ��κ��������ʼ�����ý���� ��3����������ɵ�x1="k" +1��x2=k+2��������AB=k+1��AC=k+2���ٸ��ݹ��ɶ��������з�����⣻
�ڷ�AC=BC=5��AB=BC=5�����������ϵ��������ε�������⼴��.
��1���ɷ���x2
 (2k+3)x+k2+3k+2=0����b2
(2k+3)x+k2+3k+2=0����b2 4ac=1��
4ac=1�� ��������������ȵ�ʵ������
��������������ȵ�ʵ��������2���跽��x2
 (2k+3)x+k2+3k+2=0��������Ϊ
(2k+3)x+k2+3k+2=0��������Ϊ ��
�� �����������
����������� ��
������һԪ���η��̸���ϵ���Ĺ�ϵ�ã�

 ��
�� ���ԣ���k��
 ʱ,mȡ����Сֵ
ʱ,mȡ����Сֵ ��
�� ��3����x1="k" +1��x2=k+2��������AB=k+1��AC=k+2��
 б��BC=5ʱ����AB2+AC2=BC2����(k+1)2+(k+2)2=25
б��BC=5ʱ����AB2+AC2=BC2����(k+1)2+(k+2)2=25 ���k1=2��k2=
 5(��ȥ)
5(��ȥ)  ��k="2" ʱ����ABC��ֱ�������Σ�
��k="2" ʱ����ABC��ֱ�������Σ� ��
 AB=k+1��AC=k+2��BC=5,
AB=k+1��AC=k+2��BC=5, �ɣ�1��֪AB��AC
�������������
����AC=BC=5ʱ��k+2=5��k=3��
��5��5��4�����������
 ��ABC���ܳ�Ϊ5+5+k+1=14
��ABC���ܳ�Ϊ5+5+k+1=14 ����AB=BC=5ʱ��k+1=5��k=4��
��5��5��6�����������
 ��ABC���ܳ�Ϊ5+5+k+2=16��
��ABC���ܳ�Ϊ5+5+k+2=16���ʡ�ABC���ܳ��ֱ���14��16��
����������Ĺؼ������һԪ���η��̸���������б�ʽ��
 �Ĺ�ϵ����1��
�Ĺ�ϵ����1�� ��������������ȵ�ʵ��������2��
��������������ȵ�ʵ��������2�� ������������ȵ�ʵ��������3��
������������ȵ�ʵ��������3�� ����û��ʵ������
����û��ʵ������
��ϰ��ϵ�д�
 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����Ŀ
 �Ľ���x1=0,x2=-1.__________��
�Ľ���x1=0,x2=-1.__________�� �������䷽��ȷ���ǣ� ��
�������䷽��ȷ���ǣ� ��



 �ĸ�����������ε��ܳ�Ϊ ��
�ĸ�����������ε��ܳ�Ϊ ��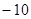 ����ԭ����Ϊ
����ԭ����Ϊ  ���䷽����
���䷽����  �Ľ�Ϊ
�Ľ�Ϊ