题目内容
(1)如图1,∠A=70°,BP、CP分别平分∠ABC和∠ACB,则∠P的度数是________.
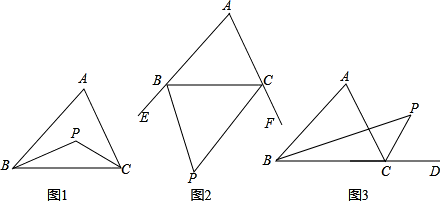
(2)如图2,∠A=70°,BP、CP分别平分∠EBC和∠FCD,则∠P的度数是________.
(3)如图3,∠A=70°,BP、CP分别平分∠ABC和∠ACD,求∠P的度数.
解:(1)∵BP、CP分别平分∠ABC和∠ACB,
∴∠PBC= ∠ABC,∠PCB=
∠ABC,∠PCB= ∠ACB,
∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB),
(∠ABC+∠ACB),
= ×(180°-∠A)=55°,
×(180°-∠A)=55°,
∴∠P=180°-(∠PCB+∠PBC)=125°,
故答案为:125°.
(2)∵∠EBC=∠A+∠ACB,∠FCB=∠A+∠ABC,
∴∠EBC+∠FCB=∠A+∠ACB+∠A+∠ABC,
=180°+70°=250°,
∵BP、CP分别平分∠EBC和∠FCD,
∴∠PBC= ∠EBC,∠PCB=
∠EBC,∠PCB= ∠FCB,
∠FCB,
∴∠PBC+∠PCB= (∠EBC+∠FCB),
(∠EBC+∠FCB),
=125°,
∴∠P=180°-(∠PBC+∠PCB)=55°,
故答案为:55°.
(3)∠ACD=∠A+∠ABC,
∵CP平分∠ACD,BP平分∠ABC,
∴∠PBC= ∠ABC,∠PCA=
∠ABC,∠PCA= ∠ACD=
∠ACD= ∠A+
∠A+ ∠ABC,
∠ABC,
∵∠P=180°-(∠PBC+∠PCA+∠ACB),
= ∠A=35°,
∠A=35°,
即∠P等于∠A的一半,
答:∠P的度数是35°.
分析:(1)根据BP、CP分别平分∠ABC和∠ACB,得到∠PBC= ∠ABC,∠PCB=
∠ABC,∠PCB= ∠ACB,求出∠PBC+∠PCB=55°,根据三角形的内角和定理求出∠P即可;
∠ACB,求出∠PBC+∠PCB=55°,根据三角形的内角和定理求出∠P即可;
(2)根据∠EBC=∠A+∠ACB,∠FCB=∠A+∠ABC,求出∠EBC+∠FCB=250°,根据BP、CP分别平分∠EBC和∠FCD,得到∠PBC= ∠EBC,∠PCB=
∠EBC,∠PCB= ∠FCB,求出∠PBC+∠PCB=125°,即可求出答案;
∠FCB,求出∠PBC+∠PCB=125°,即可求出答案;
(3)根据∠ACD=∠A+∠ABC,和CP平分∠ACD,BP平分∠ABC,得到∠PBC= ∠ABC,∠PCA=
∠ABC,∠PCA= ∠ACD=
∠ACD= ∠A+
∠A+ ∠ABC,根据∠P=180°-(∠PBC+∠PCA+∠ACB),得到
∠ABC,根据∠P=180°-(∠PBC+∠PCA+∠ACB),得到 ∠A即可.
∠A即可.
点评:本题主要考查对三角形的内角和定理,三角形的外角,角平分线的定义等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键.
∴∠PBC=
 ∠ABC,∠PCB=
∠ABC,∠PCB= ∠ACB,
∠ACB,∴∠PBC+∠PCB=
 (∠ABC+∠ACB),
(∠ABC+∠ACB),=
 ×(180°-∠A)=55°,
×(180°-∠A)=55°,∴∠P=180°-(∠PCB+∠PBC)=125°,
故答案为:125°.
(2)∵∠EBC=∠A+∠ACB,∠FCB=∠A+∠ABC,
∴∠EBC+∠FCB=∠A+∠ACB+∠A+∠ABC,
=180°+70°=250°,
∵BP、CP分别平分∠EBC和∠FCD,
∴∠PBC=
 ∠EBC,∠PCB=
∠EBC,∠PCB= ∠FCB,
∠FCB,∴∠PBC+∠PCB=
 (∠EBC+∠FCB),
(∠EBC+∠FCB),=125°,
∴∠P=180°-(∠PBC+∠PCB)=55°,
故答案为:55°.
(3)∠ACD=∠A+∠ABC,
∵CP平分∠ACD,BP平分∠ABC,
∴∠PBC=
 ∠ABC,∠PCA=
∠ABC,∠PCA= ∠ACD=
∠ACD= ∠A+
∠A+ ∠ABC,
∠ABC,∵∠P=180°-(∠PBC+∠PCA+∠ACB),
=
 ∠A=35°,
∠A=35°,即∠P等于∠A的一半,
答:∠P的度数是35°.
分析:(1)根据BP、CP分别平分∠ABC和∠ACB,得到∠PBC=
 ∠ABC,∠PCB=
∠ABC,∠PCB= ∠ACB,求出∠PBC+∠PCB=55°,根据三角形的内角和定理求出∠P即可;
∠ACB,求出∠PBC+∠PCB=55°,根据三角形的内角和定理求出∠P即可;(2)根据∠EBC=∠A+∠ACB,∠FCB=∠A+∠ABC,求出∠EBC+∠FCB=250°,根据BP、CP分别平分∠EBC和∠FCD,得到∠PBC=
 ∠EBC,∠PCB=
∠EBC,∠PCB= ∠FCB,求出∠PBC+∠PCB=125°,即可求出答案;
∠FCB,求出∠PBC+∠PCB=125°,即可求出答案;(3)根据∠ACD=∠A+∠ABC,和CP平分∠ACD,BP平分∠ABC,得到∠PBC=
 ∠ABC,∠PCA=
∠ABC,∠PCA= ∠ACD=
∠ACD= ∠A+
∠A+ ∠ABC,根据∠P=180°-(∠PBC+∠PCA+∠ACB),得到
∠ABC,根据∠P=180°-(∠PBC+∠PCA+∠ACB),得到 ∠A即可.
∠A即可.点评:本题主要考查对三角形的内角和定理,三角形的外角,角平分线的定义等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.